Untitled Document

Las actividades geométricas y de medida de magnitudes son un contexto muy apropiado para iniciar las fracciones. Veamos algunos ejemplos.

ACTIVIDADES CON EL GEOPLANO

Un geoplano es una retícula cuadrada, fácilmente materializable, por ejemplo, mediante un tablero con puntillas, que se pueden unir con gomillas (en la figura, se han unido con gomillas todos los vértices).

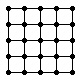
Un geoplano virtual se puede encontrar en:

http://www.matti.usu.edu/nlvm/enu/navd/frames_asid_125_g_4_t_3.html

Con un ordenador se puede simular utilizando un programa de dibujo, uniendo los puntos mediante segmentos rectos. También se puede utilizar algún programa interactivo específico.

Ejemplos de actividades:

Parte o divide un cuadrado cuyo lado tenga una longitud de 4 en dos partes iguales. ¿De cuántas formas diferentes lo puedes hacer? ¿Qué parte del total representa en cada caso, cada una de las dos partes resultantes?

Dibuja sobre el geoplano otra forma diferente (rectángulo, triángulo, hexágono, octógono,...) y repite las cuestiones anteriores.

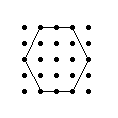
Parte o divide un cuadrado cuyo lado tenga una longitud de 3 en tres partes iguales. ¿De cuántas formas diferentes lo puedes hacer? ¿Qué parte del total representa en cada caso, cada una de las tres partes resultantes?

Parte o divide un cuadrado cuyo lado tenga una longitud de 4 en cuatro partes iguales. ¿De cuántas formas diferentes lo puedes hacer? ¿Qué parte del total representa en cada caso, cada una de las cuatro partes resultantes?
Dado un cuadrado de papel cuyo lado tenga una longitud de 4, une por los puntos medios de los lados, de manera que se obtenga un nuevo cuadrado. Compara su tamaño con el del cuadrado original. Repite el proceso con el nuevo cuadrado y compara los tamaños de los diferentes cuadrados resultantes.

Compara los tamaños de los cuadrados de lado 1, 2, 3 y 4. ¿Cuántas veces es el cuadrado de lado 4 mayor que el de lado 1, 2 ó 3? Si al cuadrado de lado 4 le damos el valor 1, ¿qué valor le daremos a los otros cuadrados?

ACTIVIDADES CON EL HEXÁGONO REGULAR

Consultar la siguiente dirección: http://www.best.com/~ejad/java/patterns/patterns_j.shtml

Actividades:

La figura siguiente es el hexágono regular. ¿Qué podrías decir de ella? ¿Qué propiedades tiene?

Las siguientes figuras pueden obtenerse como partes del hexágono regular

¿Qué podrías decir de estas figuras? ¿Qué propiedades tienen? ¿Qué relación tienen con el hexágono regular?

¿Cuántos hay en ?

¿Cuántos hay en ?

¿Cuántos hay en ?

¿Cuántos hay en ?

¿Cuántos hay en ?

¿Cuántos hay en ?

Basándote en las relaciones introducidas en la actividad anterior, responde a las siguientes cuestiones:

Si = 1, =

Si    = 1, =

Si    = 1, =

Si    = 1, =

Si es 1/2 de 1 unidad, entonces dibujar 1 unidad.

Si es 1/2 de 1 unidad, entonces dibujar 2 1/2 unidades

Si es 1/2 de 1 unidad, entonces dibujar 1 unidad

Si es 1/3 de 1 unidad, entonces dibujar 1 unidad

Si es 1/2 de 1 unidad, entonces is

ACTIVIDADES CON REGLETAS CUISENAIRE

Las regletas Cuisenaire son una colección de regletas, de planta rectangular, de diferentes tamaños y colores, si bien a una gualdad de tamaños va asociada una igualdad de colores. La más pequeña tiene una longitud de un centímetro, y las restantes aumentan de centímetro en centímetro, hasta la mayor que tiene una longitud de 10 centímetros

Puedes encontrar regletas virtuales en http://www.arcytech.org/java/integers/integers.html

Ejemplos de actividades:

Si le damos el valor 1 a la regleta blanca, ¿qué valor le daremos a las demás piezas?

: Si le damos el valor 1 a la regleta amarilla, ¿qué valor le daremos a las demás piezas?
Si le damos el valor 1 a la regleta azul, ¿qué valor le daremos a las demás piezas?
Si le damos el valor 1 a la regleta naranja, ¿qué valor le daremos a las demás piezas?

ACTIVIDADES CON EL TANGRAM

El tangram es un puzzle que resulta de partir un cuadrado en siete partes, como se indica en la figura. Puede ser usado en clase de matemáticas con diferentes finalidades. Aquí lo utilizaremos para practicar con las fracciones.

Se puede utilizar el tangram, de forma interactiva, en las siguientes direcciones:
http://www.multimania.com/casa/html/tangram.html
http://solar.aie.nl/~geert/java/public/Tangram.html

Realizar distintas figuras con todas las piezas del tangram

Si damos al triángulo más pequeño el valor 1, ¿qué valor daremos a las demás piezas?
Si damos al cuadrado el valor 1, ¿qué valor daremos a las demás piezas?
Si damos al cuadrado grande (formado con todas las piezas del tangram) el valor 1, ¿qué valor daremos a las demás piezas?
Si damos al triángulo intermedio el valor 1, ¿qué valor daremos a las demás piezas?
Si damos al paralelogramo el valor 1, ¿qué valor daremos a las demás piezas?
Si damos al triángulo más grande el valor 1, ¿qué valor daremos a las demás piezas?
Si damos al cuadrado grande el valor 1, ¿qué valor numérico le daremos a las demás piezas?
Si sumamos todos los números asociados a las figuras en la actividad anterior, ¿qué número resultará?
Formar todos los cuadrados de distinto tamaño posibles con distintas piezas del tangram. Determinar las respectivas áreas.
Formar todos los triángulos rectángulos de distinto tamaño posibles con distintas piezas del tangram. Determinar las respectivas áreas.
Formar todos los rectángulos de distinto tamaño posibles con distintas piezas del tangram. Determinar las respectivas áreas.
Formar todos los paralelogramos de distinto tamaño posibles con distintas piezas del tangram. Determinar las respectivas áreas.