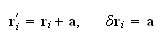
Desde tiempo remotos en física se sabe que el hecho de conocer las simetrías que posee un sistema que se desea estudiar ayuda a resolverlo. Existe una relación íntima entre las simetrías que tiene un sistema y las leyes de conservación del sistema. Por ejemplo, si un sistema es invariante antre las tralaciones entonces se conserva su momento lineal y si es invariante ante las rotaciones, se conserva su momento angular.
Vamos a ver la primera de estas propiedades desde el punto de vista clásico.
Supongamos la siguiente transformación para un sistema de partículas:
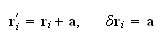
donde
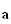 es un vector infinitesimal arbitrario. Esta transformación es
lógicamente una traslación. Si el sistema permanece invariante ante
esta transformación entonces la lagrangiana tiene que permanecer
invariante:
es un vector infinitesimal arbitrario. Esta transformación es
lógicamente una traslación. Si el sistema permanece invariante ante
esta transformación entonces la lagrangiana tiene que permanecer
invariante:
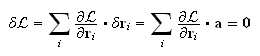
El vector
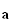 lo podemos sacar del sumatorio y utilizando las ecuaciones de Lagrange
queda:
lo podemos sacar del sumatorio y utilizando las ecuaciones de Lagrange
queda:
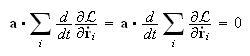
Como
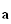 es un vector arbitrario, se verifica
que:
es un vector arbitrario, se verifica
que:
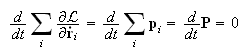
Por tanto, el momento lineal total del sistema se conserva.
De la misma forma se puede demostrar que la invariancia ante rotaciones conduce a la conservación del momento angular total. En este caso la transformación es:
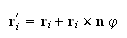
donde
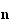 es un vector unitario arbitrario que va en la dirección alrededor de la
cual se realiza una rotación infinitesimal de un ángulo
es un vector unitario arbitrario que va en la dirección alrededor de la
cual se realiza una rotación infinitesimal de un ángulo
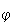 arbitrario.
arbitrario.
En mecánica cuántica, sin embargo, es más sencillo ver la relación que existe entre las simetrías y las leyes de conservación. Las operaciones de simetría (traslaciones, rotaciones, ...) conservan la norma del vector de estado (o función de onda si estamos en la representación coordenadas), de modo que están representadas por operadores unitarios, es decir, operadores que verifican la condición:
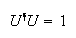
La ecuación de Schrödinger es:
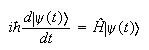
Supongamos una transformación de simetría representada por el
operador unitario
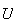 .
Si el sistema queda invariante ante la transformación, entonces el
vector:
.
Si el sistema queda invariante ante la transformación, entonces el
vector:
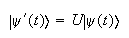
también tiene que verificar la ecuación de Schrödinger si
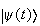 la verifica, de modo
que:
la verifica, de modo
que:
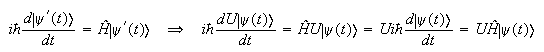
Por tanto, se tiene que cumplir que:
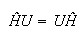
por tanto el operador hamiltoniano conmuta con
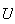 .
Esta última ecuación también se puede escribir como
.
Esta última ecuación también se puede escribir como
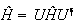 ,
que nos indica que el hamiltoniano es invariante ante la transformación
de simetría. Ahora bien, qué relación hay con las leyes de
conservación? ya que aunque el hamiltoniano conmute con
,
que nos indica que el hamiltoniano es invariante ante la transformación
de simetría. Ahora bien, qué relación hay con las leyes de
conservación? ya que aunque el hamiltoniano conmute con
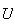 no es una constante del movimiento ya que no tiene por qué ser
hermítico. Muchas transformaciones de simetría dependen de uno o
varios parámetros que indicaremos como
no es una constante del movimiento ya que no tiene por qué ser
hermítico. Muchas transformaciones de simetría dependen de uno o
varios parámetros que indicaremos como
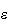 (en la translación sería la distancia y dirección de la
traslación, en la rotación la dirección y en ángulo de
giro,...), de forma que
(en la translación sería la distancia y dirección de la
traslación, en la rotación la dirección y en ángulo de
giro,...), de forma que
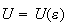 y de modo que
y de modo que
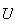 tiende a la unidad cuando
tiende a la unidad cuando
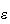 tiende a cero (esto no es cierto para ciertas transformaciones como la
inversión espacial). Si consideramos valores de
tiende a cero (esto no es cierto para ciertas transformaciones como la
inversión espacial). Si consideramos valores de
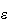 infinitesimales y desarrollamos
infinitesimales y desarrollamos
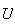 en potencias de
en potencias de
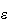 ,
podemos escribir los dos primeros términos de la
forma:
,
podemos escribir los dos primeros términos de la
forma:
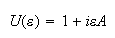
Pues bien, si
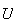 es unitario hasta primer orden en
es unitario hasta primer orden en
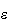 entonces se puede ver que
entonces se puede ver que
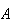 tiene que ser hermítico, y si
tiene que ser hermítico, y si
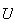 conmuta con el hamiltoniano, también lo hará el operador
conmuta con el hamiltoniano, también lo hará el operador
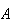 (
(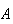 pueden ser varios operadores si
pueden ser varios operadores si
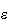 son varios parámetros, de modo que habrá un operador por cada
parámetro). Por tanto, ya tenemos la constante del movimiento, que es el
operador hermítico
son varios parámetros, de modo que habrá un operador por cada
parámetro). Por tanto, ya tenemos la constante del movimiento, que es el
operador hermítico
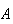 .
Este operador se denomina el generador de la transformación de
simetría. En el caso de las traslaciones el generador es el operador
momento lineal y en las rotaciones el momento angular.
.
Este operador se denomina el generador de la transformación de
simetría. En el caso de las traslaciones el generador es el operador
momento lineal y en las rotaciones el momento angular.
La ventaja de este tratamiento cuántico es que es genérico y no
depende de cual sea la transformación
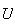 .
.