| En esta vida todo es cuestión de medida - El problema de la medida en Física Cuántica |
|
Comprender el cómo se realiza una medida es fundamental para poder entender los problemas que se están planteando actualmente sobre la interpretación de la teoría cuántica, como la decoherencia y las medidas débiles, que han permitido analizar experimentalmente la paradoja de Hardy. El esquema que se utiliza para analizar el proceso de medida en mecánica cuántica parte del formalismo desarrollado por Von Neumann. De acuerdo con este esquema, el proceso de medida consiste en producir una interacción entre el sistema en el que queremos medir y nuestro aparato de medida. Después de la interacción, el aparato de medida nos dará la información que necesitamos conocer sobre el sistema. La originalidad de tratamiento de Von Neumann consiste en que trata tanto el sistema como el aparato de medida desde el punto de vista cuántico, mientras que en la interpretación de Copenhage el aparato de medida se trataba como un objeto puramente clásico. Supongamos que tenemos un sistema S, descrito mediante un vector de un espacio de estados ES, de modo que una base del espacio de estados la constituyen los vectores {|si>}. Vamos a suponer que estos vectores son los autovectores del operador que representa a la magnitud que queremos medir. De la misma forma, nuestro aparato de medida A estará descrito mediante un vector de un espacio de estados EA, de modo que una base del espacio de estados la constituyen los vectores {|ai>}. Si nuestro aparato de medida es un objeto macroscópico, tendrá muchísimos más grados de libertad que el sistema S, sin embargo, ambos admiten una descripción cuántica. Partimos del sistema en el estado |si>, y el aparato de medida en la situación de reposo |a0>. El conjunto sistema-aparato se describe mediante un nuevo espacio de estados, que será el producto tensorial de los dos espacios, es decir, E=Es×EA. El vector de este espacio de estados que describe nuestra situación inicial será |si>×|a0>. Pues bien, si nuestro aparato de medida está calibrado, el hamiltoniano de interacción entre el sistema y el aparato de medida realizará la sisguiente evolución temporal en el conjunto sistema-aparato: |si>×|a0> → |si>×|ai> de modo que el estado del aparato ha pasado a ser el vector |ai>, que nos informa que el estado del sistema era el vector |si>. 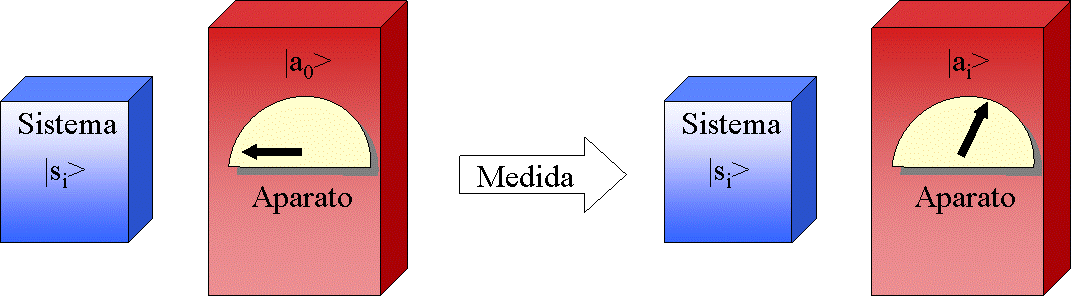
Ahora bien, ¿Qué ocurre si el estado inicial es una combinación lineal de los vectores |si>? En este caso, el estado del conjunto sistema aparato antes de la medida será: ∑ici|si>×|a0> Debido al hamiltoniano de interacción entre el sistema y el aparato de medida, se produrirá la siguiente evolución: ∑ici|si>×|a0> → ∑ici|si>×|ai> Por tanto, en este caso el hamiltoniano de interacción ha entrelazado el sistema y el aparato de medida. Sin embargo, todavía no se ha producido la medida, ya que el aparato no se encuentra en un estado bien definido. Por este motivo, la evolución anterior se denomina normalmente premedida. Una vez que colapsamos el estado del aparato y obtenemos un valor concreto, por ejemplo aj, el estado del sistema también queda colapsado, de modo que (sin tener en cuenta la evolución temporal que pueda tener el sistema entre la premedida y la medida real) el sistema se encontrará en el estado |sj>. La probabilidad de que ocurra este último proceso de colapso vale |cj|2, tal como indica la interpretación de Copenhage. Hay que destacar que la evolución temporal que tiene lugar en el colapso es absolutamente distinta a la que predice la ecuación de Schrödinger. En esta última, siempre se conserva la norma del estado a lo largo de la evolución temporal, mientras que en el colapso no se tiene por qué conservar. Pues nada, que en esta vida todo es cuestión de medida, como dijo Nacho Vidal en su primer casting. |
| Actualizado ( Viernes, 13 de Marzo de 2009 15:28 ) |


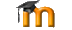





 Uno de los problemas fundamentales en el estudio de la teoría cuántica consiste en analizar cómo se realiza una medida y cómo se pasa del mundo subatómico, en el que dominan y gobiernan los fenómenos cuánticos (superposición, interferencia, entrelazamiento, etc), al mudo macroscópico de nuestro aparato de medida, en el que gobierna la mecánica de Newton.
Uno de los problemas fundamentales en el estudio de la teoría cuántica consiste en analizar cómo se realiza una medida y cómo se pasa del mundo subatómico, en el que dominan y gobiernan los fenómenos cuánticos (superposición, interferencia, entrelazamiento, etc), al mudo macroscópico de nuestro aparato de medida, en el que gobierna la mecánica de Newton.
Ese sistema macro se define cuando el foton que lanza el aparato para medir integra lo que se queria observar al sistema macro que originó la señal.
El resultado de la medicion es ese nuevo sistema integrado.
No es la funcion de onda que sí es un sistema determinado: el resultado es el nuevo sistema integrado por el medidor y la funcion de onda que quiere medir.
De ahí se infiere la decoherencia pero si bien soluciona tambien plantea otros problemas que exceden el tema