| Puede ser un átomo coherente? |
|
El límite clásico lo hemos analizado en el último tema, en el apartado "El límite clásico de la ecuación de Schrödinger". Aunque en el tema parece todo bien establecido, hay algunos puntos oscuros en este límite clásico, que de hecho todavía se siguen investigando.
El principio de correspondencia nos dice que la teoría cuántica tiende a la clásica cuando podamos considerar la constante de Planck como pequeña, lo cual suele ocurrir para números cuánticos grandes. Pero si nos fijamos en un problema bien establecido como el oscilador armónico, resulta que por muy grande que sea el número cuántico (energía) de un estado estacionario, seguirá siendo estacionario y este tipo de estados no tienen correspondencia clásica. Sin embargo, para el caso del oscilador armónico existen una serie de estados para los cuales la partícula se comporta de la misma forma que una partícula clásica. Estos estados se denominan estados coherentes cuasi-clásicos y para los cuales el paquete de ondas se mueve sin deformarse, siguiendo el movimiento del oscilador armónico simple. Estos estados se pueden ver en la aplicación "Movimiento de un paquete de ondas en el potencial del oscilador armónico", si escogemos en la parte inferior derecha un determinado valor medio para la energía del oscilador. Se puede demostrar (problema 34 de los propuestos) que estos estados son los autovectores del operador aniquilación. Desde que Schrödinger propuso la ecuación de ondas, que tanto éxito tuvo para describir el átomo de hidrógeno, él y Lorentz se plantearon si existirían estados coherentes cuasi-clásicos para el átomo de hidrógeno. En estos estados el paquete de ondas se movería sin deformarse siguiento la trayectoria elíptica de la mecánica clásica para el problema de los dos cuerpos. El hecho es que no los encontraron. Para estudiar el límite clásico de un átomo se utilizan estados muy excitados (grandes números cuánticos) y los átomos que se encuentran en estos estados excitados se denominan átomos de Rydberg. En la figura de arriba se muestra uno de estos átomos, en los que el electrón externo se encuentra muy alejado del núcleo. Estos estados se han reproducido experimentalmente. Sin embargo no son estados coherentes cuasi-clásicos, ya que si bien el electrón se encuentra bien localizado inicialmente, al cabo de unas cuantas órbitas de dispersa el paquete de ondas y se deslocaliza. Al cabo de un cierto tiempo se vuelve a recuperar el estado inicial, en lo que se denomina "reminiscencia", pero lógicamente se dispersa de nuevo. Estas reminiscencias se han medido experimentalmente. Estos átomos de Rydberg no son estados coherentes cuasi-clásicos.
En el terreno cuántico se ha conseguido reproducir estos puntos de Lagrange aplicando a un átomo de Rydberg un campo de microondas circularmente polarizado y que rota sincronizado con el electrón. Al contrario de lo que ocurre con un átomo de Rydberg, el paquete de ondas del electrón no se dispersa, de modo que electrón permanece localizado, tal como ocurre en los estados coherentes cuasi-clásicos del oscilador armónico. PD.- Gracias a Antonio Sarsa por la noticia |
| Actualizado ( Miércoles, 18 de Marzo de 2009 16:18 ) |


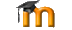





 Uno de los problemas que siempre ha fascinado a los físicos dentro de la teoría cuántica, desde sus orígenes, consiste en analizar cómo la teoría cuántica tiende a la mecánica clásica bajo cierto límite, en lo que se conoce como el límite clásico. Bohr lo denominó el principio de correspondencia.
Uno de los problemas que siempre ha fascinado a los físicos dentro de la teoría cuántica, desde sus orígenes, consiste en analizar cómo la teoría cuántica tiende a la mecánica clásica bajo cierto límite, en lo que se conoce como el límite clásico. Bohr lo denominó el principio de correspondencia. Pues bien, recientemente se han encontrado estados que si permanecen estables. Se trata de utilizar los puntos de Lagrange que aparecen cuando un satélite se encuentra en órbita en un sistema como el Tierra-Sol. Los cinco puntos de Lagrange se muestran en la figura de la derecha. Si se coloca un satélite pequeño en cualquiera de los cinco puntos permenecerá estable.
Pues bien, recientemente se han encontrado estados que si permanecen estables. Se trata de utilizar los puntos de Lagrange que aparecen cuando un satélite se encuentra en órbita en un sistema como el Tierra-Sol. Los cinco puntos de Lagrange se muestran en la figura de la derecha. Si se coloca un satélite pequeño en cualquiera de los cinco puntos permenecerá estable.
* Física Cuántica
* Mecánica Cuántica
* Utilidades
* Noticias
* Blog ... de todo un poco
* Suscripción al Blog
* Quien.es?
* Contactar
Enlaces
UcoFísica UcoFísica
UCO UCO
Moodle Moodle
Ciencias Ciencias
Dpto. Física Dpto. Física
Cinco Siglos Cinco Siglos
Experiencias musicales y otras Experiencias musicales y otras
GMail GMail
... más enlaces
Novedades
* aislador conductor
* vacaciones
* Ordenadores cuánticos
Google
Google
Buscar en la página
Artículos más visitados
* Qué rayos ¡el campo eléctrico terrestre existe!
* Entrelazamiento cuántico
* Desarrollo multipolar del potencial eléctrico
* Que puntazo la cuántica! (quantum dots; puntos cuánticos)
* No Dolly - Teorema de la no clonación cuántica
Puede ser un átomo coherente?
Átomo de RydbergUno de los problemas que siempre ha fascinado a los físicos dentro de la teoría cuántica, desde sus orígenes, consiste en analizar cómo la teoría cuántica tiende a la mecánica clásica bajo cierto límite, en lo que se conoce como el límite clásico. Bohr lo denominó el principio de correspondencia.
El límite clásico lo hemos analizado en el último tema, en el apartado "El límite clásico de la ecuación de Schrödinger". Aunque en el tema parece todo bien establecido, hay algunos puntos oscuros en este límite clásico, que de hecho todavía se siguen investigando.