Introducción
Para el ser humano es importante contar lo que tiene, lo que quiere, lo que necesita, lo que comparte, lo que da. Esa fue la razón que tuvo para crear números y formó el conjunto de los números naturales:
N = { 1, 2, 3, 4 ...}
Luego, necesitó expresar con cifras el conjunto vacío, es decir,
identificar que no había nada, no quedaba nada o no faltaba nada. Amplió,
así, el conjunto N:
N = { 0, 1, 2, 3, 4...}
En N resolvió operaciones: agregó, quitó, dividió, multiplicó... Sin embargo, se le presentaron otros problemas: ¿Cómo indicar temperaturas bajo 0? ¿Cómo diferenciar alturas y profundidades de la tierra? ¿Cómo expresar que quedó debiendo algo?
Para responder a estas interrogantes, formó otro conjunto numérico, en el que podrían expresarse cantidades menores que 0. Es el llamado conjunto de los números enteros y que se identifica con el símbolo Z.
El conjunto de los números enteros permite expresar 12° bajo 0 como: -12° y se lee menos 12. También, si se debe 5.000 euros, decir - 5.000 euros, que se lee menos 5.000 euros; o si retrocedemos 49, señalar -49.
De esta manera, el ámbito numérico se nos agranda hacia la izquierda de la recta numérica, donde el 0 es el origen.
Los números enteros se pueden definir formalmente como clases de equivalencia de pares de números naturales. Aquí prescindiremos de esa definición formal y simplemente introduciremos los números enteros ampliando la recta numérica.
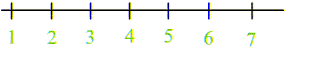
Ubicaremos los enteros que ya conocemos, por convención, a la derecha del 0, y ahora los llamaremos enteros positivos. Estos números no necesitan llevar signo + , pero para identificarlos mejor, los escribiremos con su signo.
Al conjunto de los enteros positivos se le reconoce como Z+.
Hacia la izquierda del 0, colocaremos los números enteros negativos. Estos van a la misma distancia del 0 que los enteros positivos.
A los enteros negativos no les puede faltar el signo - . Los enteros negativos
se simbolizan como Z-.
Como los enteros negativos están a la misma distancia del 0 que los positivos, se les llama opuestos. Entonces, -3 es el opuesto de +3
Para incluir un método que nos facilite la obtención de la suma, nuevamente recurriremos a la recta numérica.

Por ejemplo, sumaremos +1 + +2 . A partir del +1 nos correremos 2 lugares en sentido positivo, es decir, hacia la derecha, porque el sumando es +2.
Esto quiere decir que si sumamos enteros positivos, obtenemos un número
positivo que corresponde a la suma de sus valores absolutos.
+1 + +2 = +3
Analicemos un segundo ejemplo: -3 + -4. A partir de -3 avanzaremos 4 lugares en sentido negativo, hacia la izquierda, porque el otro sumando tiene signo negativo. De esta manera:
Este resultado nos permite determinar que si sumamos enteros negativos, obtenemos
un entero negativo equivalente a la suma de los valores absolutos de los sumandos.
-3 + -4 = -7
Ahora, obtendremos la suma de -2 + +7. En la recta numérica
Desde el -2 contamos 7 en sentido positivo, porque el otro sumando es +7. Obtenemos una suma de +5.
Ahora, sumaremos +2 + -4:
A partir de +2 contamos 4 lugares en sentido negativo, porque tenemos a -4 como sumando. El resultado es -2.
Entonces, si sumamos 2 enteros con distinto signo, restamos sus valores absolutos y conservamos el signo del que tiene el valor absoluto mayor. Comprobémoslo a continuación.
-2 + +7
La diferencia entre 7 y 2 es 5. Valor absoluto mayor es 7, entonces queda el 5 con el signo del +7, es decir, el resultado es +5.
Otra forma de determinar la suma es ocupar 2 palabras claves: debo, para los enteros negativos; y tengo, para los positivos. Así:
-3 + -1 será debo 3 y debo 1, entonces, debo 4 = -4.
+2 + +6: tengo 2 y tengo 6; tengo 8 = +8.
-5 + +3 : debo 5 y tengo 3; pago y me queda que debo 2 = -2.
-1 + +6: debo 1 y tengo 6; pago y me queda que tengo 5 = +5.
Propiedades de la adición en Z
En el conjunto de los números enteros se cumplen todas las propiedades
conocidas para la adición de números naturales. Estas son: clausura,
conmutatividad, asociatividad y elemento neutro.
En ejemplos:
-2 + -8 = -10 Clausura, porque toda adición tiene resultado.
-6 + +2 = +2 + -6 Conmutativa, porque el orden de los sumandos no cambia la
suma.
(-3 + +4) + -2 = -3 + (+4 + -2) Asociativa, porque sólo podemos sumar
2 números a la vez, y lo representamos con paréntesis.
+8 + 0 = +8 Elemento neutro el 0, porque cualquier entero sumado con 0 tiene
como suma a dicho entero.
Elemento inverso aditivo
En la adición de enteros aparece una nueva propiedad conocida como elemento inverso aditivo. Se llama así al número que, sumado con otro, nos da como suma el elemento neutro.
En otras palabras, será sumar 2 números enteros cuya suma nos dé 0.
¿Cuáles serán los números que cumplan esa condición?
Sumemos:
+6 + -6 = 0
-18 + +18 = 0
Quiere decir que llamamos elemento inverso aditivo al opuesto de un número entero.
Entonces, el inverso aditivo de -327 es +327 y el inverso aditivo de +4 es
-4, etcétera.
La sustracción en Z
A partir del conjunto Z, la sustracción ya no se resuelve como tal, porque aplicamos la propiedad del elemento inverso aditivo.
¿Cómo es eso? Si tenemos una sustracción, la cambiamos
por adición del inverso aditivo del entero que ocupa el lugar del sustraendo.
Veamos un ejemplo:
+8 - +3 ----> cambiamos el - de la operación por + y en lugar de +3 ponemos su inverso -3.
Nos queda: +8 + -3 =
A continuación, resolvemos la adición obteniendo como resultado +5.
Realizaremos el siguiente ejercicio:
-5 - -6 - +7
Aplicamos adición de inversos aditivos y nos queda:
-5 + +6 + -7 = -6.