Introducción
El concepto de número natural, pese a su aparente simplicidad, es un concepto complejo, difícil de definir. Gomez Alfonso, en su libro "Números y operaciones" (Ed. Síntesis. Madrid. 1988), sintetiza esta dificultad para definir el número natural, indicando que la pregunta acerca de qué es un número:
Es una de esas preguntas cuya respuesta suele soslayarse. ¡Todo el mundo sabe qué cosa es el número! Ahora bien, si se reitera la pregunta, unos guardarán silencio, otros se justificarán diciendo que lo que les pasa es que no tienen palabras para explicarse, y los más, bueno, los más....
Aun no sabiendo lo que es el número, muchos aceptarán que el 6 lo es y que también lo es el VI, y también IIIIII; y que todas esas cosas son el mismo número. Pero esto no puede ser, ya que son objetos distintos, y objetos distintos no pueden ser la misma cosa. Decir que 6 no es un número, es como decir que Pepe no es un nombre. ¡Es cierto, 6 es sólo el nombre de un número, como Pepe es el nombre de un hombre!
Aclarado esto, volvamos a donde estábamos: ¿Qué es el número?
Lo primero que conviene advertir es que los números no existen en la vida real, en la naturaleza, en la sociedad. El concepto de número natural es un concepto abstracto, que sólo existe en nuestra mente, aunque lo usamos para representar situaciones de la vida real. Es una propiedad que asociamos a los conjuntos de objetos, para referir aspectos cuantitativos u ordinales.
Desde un punto de vista matemático, la definición de número natural se suele hacer atendiendo a su aspecto cardinal o a su aspecto ordinal.
La definición del número natural como cardinal de una clase de conjuntos se sustenta en la teoría de conjuntos, desarrollada por Cantor entre 1874 and 1897. Las ideas básicas pueden consultarse en http://www.uwec.edu/academic/curric/andersrn/cardinalweb.htm
La siguiente definición de número natural, presentada en una enciclopedia electrónica, se centra en su aspecto cardinal:
(El número natural es) Un concepto abstracto que simboliza cierta propiedad común a todos los conjuntos coordinables entre si. (http://www.memo.com.co/fenonino/aprenda/matemat/matematicas6.html)
Otra forma de definir el número natural es atendiendo a su aspecto ordinal. Por ejemplo, la definición axiomatizada del número natural de Peano, que es la forma actual más utilizada para definir matemáticamente los números naturales.
Sistemas de numeración. Los sistemas de numeracion a lo largo de
la historia
(Siguiendo básicamente a Juan Casado, http://thales.cica.es/rd/Recursos/rd97/Otros/SISTNUM.html
Introducción. El Concepto de Base
Cuando los hombres empezaron a contar usaron los dedos, guigarros, marcas en bastones, nudos en una cuerda y algunas otras formas para ir pasando de un número al siguiente. A medida que la cantidad crece se hace necesario un sistema de representación más práctico.
En diferentes partes del mundo y en distintas épocas se llegó a la misma solución, cuando se alcanza un determinado número se hace una marca distinta que los representa a todos ellos. Este número es la base. Se sigue añadiendo unidades hasta que se vuelve a alcanzar por segunda vez el número anterior y se añade otra marca de la segunda clase. Cuando se alcanza un número determinado (que puede ser diferente del anterior constituyendo la base auxiliar) de estas unidades de segundo orden, las decenas en caso de base 10, se añade una de tercer orden y así sucesivamente.
La base que más se ha utilizado a lo largo de la Historia es 10 según todas las apariencias por ser ese el número de dedos con los que contamos. Hay alguna excepción notable como son las numeración babilónica que usaba 10 y 60 como bases y la numeración maya que usaba 20 y 5 aunque con alguna irregularidad.
Desde hace 5000 años la gran mayoría de las civilizaciones han contado en unidades, decenas, centenas, millares etc. es decir de la misma forma que seguimos haciéndolo hoy. Sin embargo la forma de escribir los números ha sido muy diversa y muchos pueblos han visto impedido su avance científico por no disponer de un sistema eficaz que permitiese el cálculo.
Casi todos los sistemas utilizados representan con exactitud los números
enteros, aunque en algunos pueden confundirse unos números con otros,
pero muchos de ellos no son capaces de representar grandes cantidades, y otros
requieren tal cantidad de simbolos que los hace poco prácticos.
Pero sobre todo no permiten en general efectuar operaciones tan sencillas
como la multiplicación, requiriendo procedimientos muy complicados
que sólo estaban al alcance de unos pocos iniciados. De hecho cuando
se empezó a utilizar en Europa el sistema de numeración actual,
los abaquistas, los profesionales del cálculo se opusieron con las
más peregrinas razones, entre ellas la de que siendo el cálculo
algo complicado en sí mismo, tendría que ser un metodo diabólico
aquel que permitiese efectuar las operaciones de forma tan sencilla.
El sistema actual fue inventado por los indios y transmitido a Europa por los árabes. El gran mérito fue la introducción del concepto y símbolo del cero, lo que permite un sistema en el que sólo diez simbolos puedan representar cualquier número por grande que sea y simplificar la forma de efectuar las operaciones.
Sistemas de Numeracion Aditivos
Para ver cómo es la forma de representación aditiva consideremos el sistema geroglífico egipcio. Por cada unidad se escribe un trazo vertical, por cada decena un símbolo en forma de arco y por cada centena, millar, decena y centena de millar y millón un geroglífico específico. Así para escribir 754 usaban 7 geroglíficos de centenas 5 de decenas y 4 trazos. De alguna forma todas las unidades están fisicamente presentes.
Los sistemas aditivos son aquellos que acumulan los simbolos de todas las unidades, decenas... como sean necesarios hasta completar el número. Una de sus características es por tanto que se pueden poner los símbolos en cualquier orden, aunque en general se ha preferido una determinada disposición.
Han sido de este tipo las numeraciones egipcia, sumeria (de base 60), hitita, cretense, azteca (de base 20), romana y las alfabéticas de los griegos, armenios, judios y árabes.
El Sistema de Numeración Egipcio
Desde el tercer milenio A.C. los egipcios usaron un sistema deescribir los números en base diez utilizando los geroglíficos de la figura para representar los distintos ordenes de unidades.
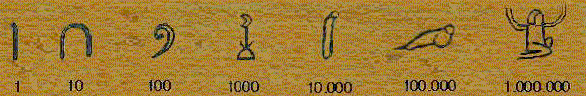
Se usaban tantos de cada uno cómo fuera necesario y se podian escribir indistintamente de izquierda a derecha, al revés o de arriba abajo, cambiando la orientación de las figuras según el caso.
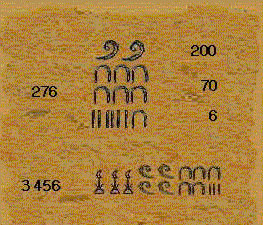
Al ser indiferente el orden se escribían a veces según criterios estéticos, y solían ir acompañados de los geroglíficos correspondientes al tipo de objeto (animales, prisioneros, vasijas etc.) cuyo número indicaban. En la figura aparece el 276 tal y como figura en una estela en Karnak.
Estos signos fueron utilizados hasta la incorporación de Egipto al imperio romano. Pero su uso quedó reservado a las inscripciones monumentales, en el uso diario fue sustituido por la escritura hierática y demótica, formas más simples que permitian mayor rapidez y comodidad a los escribas.
En estos sistemas de escritura los grupos de signos adquirieron una forma propia, y asi se introdujeron símbolos particulares para 20, 30....90....200, 300.....900, 2000, 3000...... con lo que disminuye el número de signos necesarios para escribir una cifra.
El sistema de numeración romano
Los números romanos son una sucesión de las letras mayúsculas I, V, X, L, C, D, y M (denotando 1, 5, 10, 50, 100, 500 and 1000, respectivamente) Los primero 20 números romanos son:
I = = 1; II = 1+1 = 2; III = 1+1+1 = 3; IV = 5-1 = 4; V = = 5; VI = 5+1 = 6; VII = 5+(1+1) = 7; VIII = 5+(1+1+1) = 8; IX = 10-1 = 9; X = = 10; XI = 10+1 = 11; XII = 10+(1+1) = 12; XIII = 10+(1+1+1) = 13; XIV = 10+(5-1) = 14; XV = 10+5 = 15; XVI = 10+(5+(1)) = 16; XVII = 10+(5+(1+1) = 17; XVIII = 10+(5+(1+1+1)) = 18; XIX = 10+(10-1) = 19; XX = 10+10 = 20
En general, los números romanos pueden ser automáticamente convertidos a nuestro sistema habitual asignando un valor numérico a cada letra, de acuerdo con la tabla de abajo y calculando el total
M=1000 | D=500 | C=100 | L=50 | X=10 | V=5 | I=1
En todo caso, hay que tener en cuenta el principio de substracción, el cual requiere que un número más pequeño que aparezca antes que uno mayor debe ser substraído del valor más alto, no sumado al total. Por ejemplo, IX es el número romano correspondiente a 9 (esto es, 10 - 1).
Otra convención es que un signo no puede ser usado más de tres veces seguida, salvo el M (puesto que el sistema romano no tiene símbolos para números mayores de 1000).
El Sistema de Numeración Griego
El primer sitema de numeración griego se desarrolló hacia el 600 A.C. Era un sistema de base decimal que usaba los símbolos de la figura siguiente para representar esas cantidades. Se utilizaban tantas de ellas como fuera necesario según el principio de las numeraciones aditivas.

Para representar la unidad y los números hasta el 4 se usaban trazos verticales. Para el 5, 10 y 100 las letras correspondientes a la inicial de la palabra cinco (pente), diez (deka) y mil (khiloi). Por este motivo se llama a este sistema acrofónico.
Los símbolos de 50, 500 y 5000 se obtienen añadiendo el signo de 10, 100 y 1000 al de 5, usando un principio multiplicativo. Progresivamente este sistema ático fue reemplazado por el jónico, que empleaba las 24 letras del alfabeto griego junto con algunos otros símbolos según la tabla siguiente

De esta forma los números parecen palabras, ya que están compuestos por letras, y a su vez las palabras tienen un valor numérico, basta sumar las cifras que corresponden a las letras que las componen. Esta circunstancia hizo aparecer una nueva suerte de disciplina mágica que estudiaba la relación entre los números y las palabras. En algunas sociedades como la judía y la árabe, que utilizaban un sistema similar, el estudio de esta relación ha tenido una gran importancia y ha constituido una disciplina aparte: la kábala, que persigue fines místicos y adivinatorios.
Sistemas de Numeracion Híbridos
En estos sistemas se combina el principio aditivo con el multiplicativo. Si para representar 500 los sistemas aditivos recurren a cinco representaciones de 100, los híbridos utilizan la combinación del 5 y el 100. Pero siguen acumulando estas combinaciones de signos para los números más complejos. Por lo tanto sigue siendo innecesario un símbolo para el 0. Para representar el 703 se usa la combinacion del 7 y el 100 seguida del 3.
El orden en la escritura de las cifras es ahora fundamental para evitar confusiones, se dan así los pasos para llegar al sistema posicional, ya que si los signos del 10, 100 etc se repiten siempre en los mismos lugares, pronto alguien piensa en suprimirlos, dándolos por supuestos y se escriben sólo las cifras correspondientes a las decenas, centenas etc. .Pero para ello es necesario un cero, algo que indique que algún orden de magnitud está vacío y no se confundan el 307 con 370, 3070 ...
Además del chino clásico han sido sistemas de este tipo el asirio, arameo, etíope y algunos del subcontinente indio cómo el tamil, el malayalam y el cingalés.
El Sistema de Numeración Chino
La forma clásica de escritura de los números en China se empezó a usar desde el 1500 A.C. aproximadamente. Es un sistema decimal estricto que usa las unidades y los distintas potencias de 10. Utiliza los ideogramas de la figura

y usa la combinación de los números hasta el diez con la decena, centena, millar y decena de millar para según el principio multiplicativo representar 50, 700 ó 3000. El orden de escritura se hace fundamental,ya que 5 10 7 igual podría representar 57 que 75.
Tradicionalmente se ha escrito de arriba abajo aunque también se hace de izquierda a derecha como en el ejemplo de la figura.
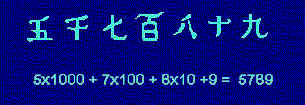
No es necesario un símbolo para el cero siempre y cuando se pongan
todos los ideogramas, pero aún así a veces se suprimían
los correspondientes a las potencias de 10.
Aparte de esta forma que podríamos llamar canónica se usaron
otras. Para los documento importantes se usaba una grafía más
complicada con objeto de evitar falsificaciones y errores. En los sellos se
escribía de forma más estilizada y lineal y aún se usaban
hasta dos grafías diferentes en usos domésticos y comerciales,
aparte de las variantes regionales. Los eruditos chinos por su parte desarrollaron
un sistema posicional muy parecido al actual que desde que incorporó
el cero por influencia india en s. VIII en nada se diferencia de este.
Sistemas de Numeración Posicionales
Mucho más efectivos que los sistemas anteriores son los posicionales. En ellos la posición de una cifra nos dice si son decenas, centenas ... o en general la potencia de la base correspondiente.
Sólo tres culturas además de la india lograron desarrollar un sistema de este tipo. Babilonios, chinos y mayas en distintas épocas llegaron al mismo principio. La ausencia del cero impidió a los chinos un desarrollo completo hasta la intraducción del mismo. Los sistemas babilónico y maya no eran prácticos para operar porque no disponían de simbolos particulares para los dígitos, usando para representarlos una acumulación del signo de la unidad y la decena. El hecho que sus bases fuese 60 y 20 respectivamente no hubiese representado en principio nigún obstáculo. Los mayas por su parte cometían una irregularidad a partir de las unidades de tercer orden, ya que detrás de las veintenas no usaban 20x20=400 sino 20x18=360 para adecuar los números al calendario, una de sus mayores preocupaciones culturales.
Fueron los indios antes del siglo VII los que idearon el sistema tal y como hoy lo conocemos, sin mas que un cambio en la forma en la que escribimos los nueve dígitos y el cero. Aunque con frecuencia nos referimos a nuestro sistema de numeración cómo árabe, las pruebas arqueológicas y documentales demuestran el uso del cero tanto en posiciones intermedias como finales en la India desde el sss. Los árabes transmitieron esta forma de representar los números y sobre todo el cáculo asociado a ellas, aunque tardaron siglos en ser usadas y aceptadas. Una vez más se produjo una gran resistencia a algo por el mero hecho de ser nuevo o ajeno, aunque sus ventajas eran evidentes. Sin esta forma eficaz de numerar y efectuar cálculos dificilmente la ciencia hubiese podido avanzar.
El Sistema de Numeración Babilónico
Entre la muchas civilizaciones que florecieron en la antigua Mesopotamia se desarrollaron distintos sistemas de numeración. En el ssss A.C. se inventó un sistema de base 10, aditivo hasta el 60 y posicional para números superiores. Para la unidad se usaba la marca vertical que se hacía con el punzón en forma de cuña. Se ponían tantos como fuera preciso hasta llegar a 10, que tenía su propio signo.
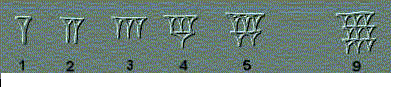
De este se usaban los que fuera necesario completando con las unidades hasta llegar a 60.
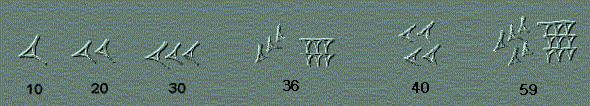
A partir de ahí se usaba un sistema posicional en el que los grupos de signos iban representando sucesivamente el número de unidades, 60, 60x60, 60x60x60 y asi sucesivamente como en los ejemplos que se acompañan.
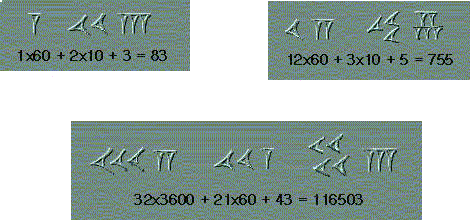
El Sistema de Numeración Maya
Los mayas idearon un sistema de base 20 con el 5 cómo base auxiliar. La unidad se representaba por un punto. Dos, tres, y cuatro puntos servían para 2, 3 y 4. El 5 era una raya horizontal, a la que seañadían los puntos necesarios para representar 6, 7, 8 y 9. Para el 10 se usaban dos rayas, y de la misma forma se continúa hasta el 20, con cuatro rayas.

Hasta aquí parece ser un sistema de base 5 aditivo, pero en realidad, considerados cada uno un solo signo, estos símbolos constituyen las cífras de un sistema de base 20, en el que hay que multiplicar el valor de cada cifra por 1, 20, 20x20, 20x20x20 ... según el lugar que ocupe, y sumar el resultado. Es por tanto un sistema posicional que se escribe a arriba abajo, empezando por el orden de magnitud mayor.

Al tener cada cifra un valor relativo según el lugar que ocupa, la presencia de un signo para el cero, con el que indicar la ausencia de unidades de algún orden, se hace imprescindible y los mayas lo usaron, aunque no parece haberles interesado el concepto de cantidad nula. Cómo los babilonios lo usaron simplemente para indicar la ausencia de otro número.
Pero los científicos mayas eran a la vez sacerdotes ocupados en la observación astronómica y para expresar los número correspondientes a las fechas usaron unas unidades de tercer orden irregulares para la base 20. Así la cifra que ocupaba el tercer lugar desde abajo se multiplicaba por 20x18=360 para completar una cifra muy próxima a la duración de un año.

El año lo consideraban dividido en 18 uinal que constaba cada uno de 20 días. Se añadían algunos festivos (uayeb) y de esta forma se conseguía que durara justo lo que una de las unidades de tercer orden del sistema numérico. Además de éste calendario solar, usaron otro de carater religioso en el que el año se divide en 20 ciclos de 13 días.
Al romperse la unidad del sistema éste se hace poco práctico para el cálculo y aunque los conocimiento astronómicos y de otro tipo fueron notables los mayas no desarrollaron una matemática más allá del calendario.
Operaciones con números naturales
La suma de números naturales se puede relacionar con la unión de conjuntos. La multiplicación se puede considerar como una suma repetida. La resta y la división son operaciones inversas de aquéllas. Se puede consultar:
http://www.surlink.com.ar/egb/links.asp?pag=http://www.escolar.com/cgibin/anti/antileech.cgi?04
http://www.surlink.com.ar/egb/links.asp?pag=http://www.escolar.com/cgibin/anti/antileech.cgi?05
http://www.surlink.com.ar/egb/links.asp?pag=http://www.escolar.com/cgibin/anti/antileech.cgi?06
Divisibilidad
Las operaciones aritméticas elementales, operaciones con números naturales, son: suma, resta, producto y cociente. La suma y la resta son operaciones inversas, relacionadas con la unión de conjuntos. El producto y el cociente son también operaciones inversas que representan, respectivamente, sumas y restas reiteradas.
Ligada a la operaciones producto y cociente está la divisibilidad. Un número A es múltiplo de otro B (o divisible por él), si se puede dividir por él, de forma exacta, de manera que existe un tercer número C que multiplicado por B da A. B se llama divisor o factor de A.
Algunos criterios de divisibilidad son bien conocidos:
DIVISIBILIDAD POR 2: Un número es divisible por dos si termina en cero o en cifra par.
DIVISIBILIDAD POR 3: Un número es divisible por tres, si la suma de sus cifras absolutas es múltiplo de tres.
DIVISIBILIDAD POR 4: fijate en las dos últimas cifras. Tienen que ser dos ceros o un número múltiplo de 4.
DIVISIBILIDAD POR 5: Un número es divisible por cinco cuando acaba en cero o en cinco.
DIVISIBILIDAD POR 6: tiene que ser divisible por 2 y por 3.
DIVISIBILIDAD POR 9: Un número es divisible por nueve cuando la suma de sus cifras es múltiplo de nueve.
DIVISIBILIDAD POR 10: tiene que terminar en cero. De manera similar, si termina en 00 es divisible por 100; si termina en 000 es divisible por 1000.
DIVISIBILIDAD POR 11: Un número es divisible por once cuando la diferencia entre la suma de las cifras que ocupa la posición par y la suma de las cifras que ocupan la posición impar son múltiplo de once.
Los divisores de un número son los números por los que aquél es divisible. Cualquier número natural admite como factores el 1 y el propio número. Si admite más factores, el número se dice compuesto. En caso contrario es primo.
Ejemplos:
Divisores de 3= {1, 3} => es primo
D(7)={1, 7} => es primo
D(9)={1, 3, 9} => no es primo, es divisible por 3 además de 1 y
9
Los números primos.¿Qué es un número primo?
Seguiremos ahora las ideas de Francisco José Belijar y Juan Pablo Martínez, contenidas en la página siguiente:
http://centros5.pntic.mec.es/ies.ortega.y.rubio/Mathis/Primos/primos.htm
Los números primos son aquellos números enteros que sólo
son divisibles por si mismos y por la unidad". Ejemplos: 1,2,3,5,7,11,13,17,19...,
-1,-2,-3,...
Un poco de historia de los números primos
Desde muy antiguo los números primos han sido objeto de interés
y estudio. Ya en la antigua Grecia
aparecen numerosos estudios.
Los pitagóricos tuvieron gran interés por ellos debido a que
pensaban que los números gobernaban el mundo y tenían propiedades
místicas y "mágicas". Los números primos, por
su naturaleza indivisible, presentan todas las características para
ser "adorados" por los discípulos de Pitágoras.
En el libro "Los
Elementos" de Euclides (300a.C.), uno de los tratados más
importantes de la historia de las matemáticas, ya aparecen estudios
sobre los números primos. El propio Euclides en su libro enuncia un
teorema importante sobre números primos:
Teorema.- Hay infinitos números primos.
Si quieres puedes ver la prueba
que hace Euclides de este teorema .Se trata de la primera prueba conocida
mediante el método de reducción al absurdo; y este método
consiste en suponer cierto lo contrario de lo que se quiere probar para llegar
a una contradicción descubriendo falsa la suposición hecha.
Hubo, y sigue habiendo muchos intentos para determinar qué números
son primos. Uno de los primeros que se conocen es un procedimiento heurístico
debido a otro importante matemático griego llamado ERATÓSTENES.
La Criba de Eratóstenes
La Criba de Eratóstenes consiste en eliminar los números que
no sean primos y que por tanto sean múltiplos de algún número.
Para obtener los 150 primeros números primos, en la siguiente tabla,
a partir del 2, se van marcando todos los números saltando de 2 en
2. A continuación, a partir del 3, todos los números de 3 en
3, y así sucesivamente. Los números que quedan on los números
primos.
La factorización
(ejemplo de uso de los números primos)
La factorización de los números naturales consiste en descomponer
un número entero cualquiera en producto de números primos.
La descomposición de los números de su factores primos facilita
la determinación de su m.c.d. y m.c.m. Ejemplo:
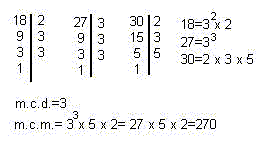
El m.c.d. es aquel número mayor y común que divide a todos ellos.
El m.c.m. es aquel número menor y común que es múltiplo a todos ellos.
Para calcular el m.c.d. se toman los factores comunes con el menor exponente y se multiplican.
Para calcular el m.c.m. se toman los factores comunes y no comunes con el mayor exponente y se multiplican. (La solución del m.c.d. y del m.c.m. está realizado en el ejemplo de arriba).
En la página web http://www.edteach.com/algebra/numbers/prime_factor_machine.html hay un procedimiento de generación de números primos.
En la página web siguiente hay un procedimiento de generación automatizada de los factores de un número. http://school.discovery.com/homeworkhelp/webmath/factint.html
En la página web siguiente hay un procedimiento de generación automatizada del máximo común divisor de dos números: http://school.discovery.com/homeworkhelp/webmath/intgcf.html