Introduction

Fuzzy Logic Systems (FLS) have been widely used thanks to their ability to successfully solve a wide range of problems in different application fields. In practice, there are almost as many FLS as different applications for which they were designed and developed. However, they usually share the following common architecture:

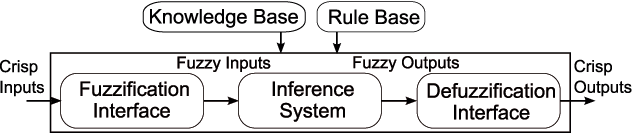
The FLS replication and application requires a high level of knowledge and experience. Furthermore, as thoroughly explained by Alcala-Fdez and Alonso few researchers publish the software and/or source code associated with their proposals, which is a major obstacle to scientific progress in other disciplines regarding both academy and industry. In recent years, open source software for FLS has been developed providing many advantages: quicker detection of errors, innovative applications, faster adoption of FLS, etc. As advised by the Task Force on Fuzzy Systems Software in the Fuzzy Systems Technical Committee of the IEEE Computational Intelligence Society, researchers and developers should think carefully about some critical considerations (interoperability, novelty, usability, and relevance) when publishing a new software.

JFML is an open source Java library which is aimed at facilitating interoperability and usability of fuzzy systems. Its novelty and relevance arise from the fact that JFML is the first library in the world which implements the new IEEE Std 1855 published and sponsored by the Standards Committee of the IEEE Computational Intelligence Society.

JFML can be freely downloaded from GitHub. To build JFML, you can clone the .git repository from git@github.com:sotillo19/JFML.git or download the library into a .zip file. We recommend following the next steps:

• Download the library into a .zip file from the Clone or Download option in GitHub or from the latest release and unzip it in a local folder.
• Create a New Java Project with Eclipse. Please, remind to select as Location the folder created in the previous step.
• Run buildJFML.xml as Ant Build with the aim of creating the project dependencies. To do so, just click the right mouse button on the xml file and then select the proper option. Notice that ant is freely available and it is usually integrated with Eclipse.
• In case of changing the source files, then run buildJAR.xml as Ant Build with the aim of compiling source files and creating the jar library.

Notice that the source code zip file already includes a compiled jar library ready to use in the Examples folder. It will be overwritten after running buildJAR.xml.

IEEE Standard 1855-2016 - Fuzzy Markup Language (FML)

Java API - JFML

We can easily create any of the four type of fuzzy system enclosed in the schema of the standard IEEE. We need to create a FuzzyInferenceSystem object with the name of the system, and then we add the definition of the knowledge base and the definition of the rule bases.

Next Java code creates a FuzzyInferenceSystem object with the name "tipper":

      FuzzyInferenceSystem tipper = new FuzzyInferenceSystem("tipper");
    

In the following subsections, we show how we can create the knowledge base and the rule bases.

Knowledge Base

At the beginning, we have to create a KnowledgeBaseType object, in which will include the definition of the system variables, and to add it to our fuzzy system:

    KnowledgeBaseType kb = new KnowledgeBaseType();
    tipper.setKnowledgeBase(kb);
  

Then, the definitions of the variables are included in the knowledge base. We can define five type of variables:

1. FuzzyVariableType: It represents an input or output fuzzy variable. Each object of this class contains the following information:
   
   
   • Name: It is a string with a unique name for the fuzzy variable. This information is required when we create the variable.
   • Scale: It is a string with the scale used to measure a fuzzy variable. This information is optional when we create the variable.
   • DomainLeft: It is a float that represents the left boundary of the universe of discourse of a fuzzy variable. This information is required when we create the variable.
   • DomainRight: It is a float that represents the right boundary of the universe of discourse of a fuzzy variable. This information is required when we create the variable.
   • Type: It is a string with the position of a fuzzy variable in a rule (consequent part or antecedent part). Its values can be "input" or "output". This information is optional when we create the variable due to that its default value is "input" when we do not indicate any value.
   • Accumulation: It is a string with the accumulation method used when this variable is involved in the consequent part of the rules. This information is optional when we create the variable. Its default value is MAX but we can select any of these accumulation methods:
     
     • MAX: Maximum
     • PROBOR: Probabilistic sum
     • BSUM: Bounded sum
     • DRS: Drastic sum
     • ESUM: Einstein sum
     • HSUM: Hamacher sum
     • NILMAX: Nilpotent maximum
     • custom_\S*: A custom accumulation method implemented by the users
     
     
   • Defuzzifier: It is a string with the defuzzifier used when this variable is involved in the consequent part of the rules. This information is optional when we create the variable. Its default value is COG but we can select any of these defuzzifiers:
   • COG: Center of gravity
   • MOM: Mean of maxima
   • LM: Leftmost maximum
   • RM: Rightmost maximum
   • COA: Center of area
   • custom_\S*: A custom defuzzifier implemented by the users
   
   
   • DefaultValue: It is a float value used only when no rule has fired for the variable at issue. This information is optional when we create the variable. Its default value is 0.
   • NetworkAddress: It is a string with the location of the fuzzy variable in a computer network. This information is optional when we create the variable. Its default value is "127.0.0.1".
   
   

   Next Java code creates a input fuzzy variable with the name "food", the left boundary 0, right boundary 10, and the default values of the rest of attributes. Moreover, this variable is added to the knowledge base of our fuzzy system:

       FuzzyVariableType food = new FuzzyVariableType("food", 0, 10);
       kb.addVariable(food);
         

   Then, we define the linguistic terms of the variable. Each term contains the attributes name (string), complement (string "true" or "false"), the type of membership function, and a float list with the parameters required for the corresponding fuzzy set. Notice that the attribute complement is optional and its default value is "false". We can define the next membership functions in JFML:

   • Triangular: This option defines the triangular function depending on three parameters a, b and c. Next Java code generates a term of this function with the name "rancid", a=0, b=2, c=4, and add it to the variable "food":
     
     

     FuzzyTermType rancid = new FuzzyTermType("rancid", FuzzyTermType.TYPE_triangularShape,(new float[] {0f, 2f, 4f}));
     food.addFuzzyTerm(rancid);
               

     
   • Left Linear: This option defines the left linear function depending on two parameters a and b. Next Java code generates a term of this function with the name "rancid", a=0, b=4, and add it to the variable "food":
     
     

     FuzzyTermType rancid = new FuzzyTermType("rancid", FuzzyTermType.TYPE_leftLinearShape,(new float[] {0f, 4f}));
     food.addFuzzyTerm(rancid);
               

     
   • Right Linear: This option defines the right linear function depending on two parameters a and b. Next Java code generates a term of this function with the name "delicious", a=4, b=10, and add it to the variable "food":
     
     

     FuzzyTermType delicious = new FuzzyTermType("delicious", FuzzyTermType.TYPE_rightLinearShape,(new float[] {4f, 10f}));
     food.addFuzzyTerm(delicious);
               

     
   • Trapezoidal: This option defines the trapezoidal function depending on four parameters a, b, c and d. Next Java code generates a term of this function with the name "rancid", a=0, b=1, c=3, d=4, and add it to the variable "food":
     
     

     FuzzyTermType rancid = new FuzzyTermType("rancid", FuzzyTermType.TYPE_trapezoidShape,(new float[] {0f, 1f, 3f, 4f}));
     food.addFuzzyTerm(rancid);
               

     
   • Rectangular Shape: This option defines the rectangular function depending on two parameters a, and b. Next Java code generates a term of this function with the name "good", a=4, b=7, and add it to the variable "food":
     
     

     FuzzyTermType good = new FuzzyTermType("good", FuzzyTermType.TYPE_rectangularShape,(new float[] {4f, 7f}));
     food.addFuzzyTerm(good);
               

     
   • Gaussian: This option defines the symmetric Gaussian function depending on two parameters c and σ. Next Java code generates a term of this function with the name "good", c=5, σ=1, and add it to the variable "food":
     
     

     FuzzyTermType good = new FuzzyTermType("good", FuzzyTermType.TYPE_gaussianShape,(new float[] {5f, 1f}));
     food.addFuzzyTerm(good);
               

     
   • Left Gaussian: This option defines the left Gaussian function depending on two parameters c and σ. Next Java code generates a term of this function with the name "rancid", c=2, σ=1, and add it to the variable "food":
     
     

     FuzzyTermType rancid = new FuzzyTermType("rancid", FuzzyTermType.TYPE_leftGaussianShape,(new float[] {2f, 1f}));
     food.addFuzzyTerm(rancid);
               

     
   • Right Gaussian: This option defines the right Gaussian function depending on two parameters c and σ. Next Java code generates a term of this function with the name "delicious", c=8, σ=1, and add it to the variable "food":
     
     

     FuzzyTermType delicious = new FuzzyTermType("delicious", FuzzyTermType.TYPE_rightGaussianShape,(new float[] {8f, 1f}));
     food.addFuzzyTerm(delicious);
               

     
   • Pi-Shaped: This spline-based curve is so named because of its Π shape and it depends on four parameters a, b, c, and d. Next Java code generates a term of this function with the name "good", a=2, b=4, c=6, d=8, and add it to the variable "food":
     
     

     FuzzyTermType good = new FuzzyTermType("good", FuzzyTermType.TYPE_piShape,(new float[] {2f, 4f, 6f, 8f}));
     food.addFuzzyTerm(good);
               

     
   • Z-Shape: This spline-based curve is so named because of its Z-shape and it depends on two parameters a, and b. Next Java code generates a term of this function with the name "rancid", a=2, b=4, and add it to the variable "food":
     
     

     FuzzyTermType rancid = new FuzzyTermType("rancid", FuzzyTermType.TYPE_zShape,(new float[] {2f, 4f}));
     food.addFuzzyTerm(rancid);
               

     
   • S-Shape: This spline-based curve is so named because of its S-shape and it depends on two parameters a, and b. Next Java code generates a term of this function with the name "delicious", a=6, b=8, and add it to the variable "food":
     
     

     FuzzyTermType delicious = new FuzzyTermType("delicious", FuzzyTermType.TYPE_sShape,(new float[] {6f, 8f}));
     food.addFuzzyTerm(delicious);
             

     
   • Singleton Shape: This option defines the singleton function depending on one parameter a. Next Java code generates a term of this function with the name "good", a=5, and add it to the variable "food":
     
     

     FuzzyTermType good = new FuzzyTermType("good", FuzzyTermType.TYPE_singletonShape,(new float[] {5f}));
     food.addFuzzyTerm(good);
               

     
   • PointSet Shape: This option defines a function by using a set of points defined by the user (piece-wise function). This function has two additional attributes (interpolationMethod and degree) and the list of parameters is a list of pointType objects defined by the user:
     • interpolationMethod: It defines the method to interpolate the points defined by the user. This attribute can table the following values: "linear" for implementing the Linear interpolation; "lagrange" for implementing the Lagrange interpolation; "spline" for implementing the Spline interpolation. This attribute is optional and its default value is "linear".
     • Degree: The polynomial degree to be employed during the interpolation process when the user selects Lagrange or Spline interpolation.

     Next Java code generates a term of this function with the name "delicious", the method to interpolate by default, and a list with the point (5, 0), (8, 0.5) and (9, 1).

     List points = new ArrayList();
      points.add(new PointType(5f, 0f));
      points.add(new PointType(8f, 0.5f));
      points.add(new PointType(9f,1f));
     
     FuzzyTermType delicious = new FuzzyTermType("delicious", FuzzyTermType.TYPE_pointSetShape, points);
     food.addFuzzyTerm(delicious);
               

     
   • Circular Definition: This option allows us to define a new term by means of a logical expression containing fuzzy terms previously defined. In this option, the list of parameters is a circular definition (CircularDefinitionType), which contains one element chosen from the following logical elements: and (AndLogicalType objects), or (OrLogicalType objects). The AndLogicalType objects have three attributes: the name of a t-norm; a name of a term of the variable or a LogicalType object (it can be AndLogicalType or OrLogicalType); and another name of a term of the variable or a LogicalType object (it can be AndLogicalType or OrLogicalType). The OrLogicalType objects have three attributes: the name of a t-conorm; a name of a term of the variable or a LogicalType object (it can be AndLogicalType or OrLogicalType); and another name of a term of the variable or a LogicalType object (it can be AndLogicalType or OrLogicalType).

     The t-norms that can be used (its default value is MIN):

     • MIN: Operator minimum
     • PROD: Operator product
     • BDIF: Bounded difference
     • DRP: Drastic product
     • EPROD: Einstein product
     • HPROD: Hamacher product
     • NILMIN: Nilpotent minimum
     • custom_\S*: A custom method
     
     

     The t-conorms that can be used(its default value is MAX):

     • MAX: Operator maximum
     • PROBOR: Probabilistic sum
     • BSUM: Bounded sum
     • DRS: Drastic sum
     • ESUM: Einstein sum
     • HSUM: Hamacher sum
     • NILMAX: Nilpotent maximum
     • custom_\S*: A custom method
     
     

     Next Java code generates a term of this function with the name "correct". It use an OrLogicalType object with the t-conorm MAX, the term "good" (created with the pi-Shaped), and the term "delicious" (created with the s-Shaped), to create the circular definition of the new term of the variable "food":

     CircularDefinitionType c = new CircularDefinitionType (new OrLogicalType ("MAX", "good", "delicious"), food);
     FuzzyTermType correct = new FuzzyTermType("correct", FuzzyTermType.TYPE_circularDefinition, c);
     food.addFuzzyTerm(correct);
             

     
   • Custom Membership Function: A custom function implemented by the users


2. AggregatedFuzzyVariableType: It represents an input fuzzy variable that can be used to aggregate two or more variables related to our system. The variables of this class contain three attributes:
   
   
   • Name: It is a string with a unique name for the fuzzy variable. This information is required when we create the variable.
   • Type: It is a string with the position of a fuzzy variable in a rule. In this type of variables, this attribute is always "input".
   • NetworkAddress: It is a string with the location of the fuzzy variable in a computer network. This information is optional when we create the variable. Its default value is "127.0.0.1".

   Next Java code creates an input fuzzy variable with the name "aggregated". Moreover, this variable is added to the knowledge base of our fuzzy system:

   AggregatedFuzzyVariableType aggregated = new AggregatedFuzzyVariableType("aggregated", "input");
   kb.addVariable(aggregated);
         

   
   

   Each variable also contains a list of AggregatedFuzzyTerm objects with the terms of the variable. Each AggregatedFuzzyTerm object has an attribute with the name of the term, and a logic object: and (AndAggregatedType) , or (OrAggregatedType). Each AndAggregatedType or OrAggregatedType object contains an only attribute t-norm (we can use the same as in the circular definition) and t-conorn (we can use the same as in the circular definition), respectively. Moreover, both objects contain any of these two elements:

   • Two ClauseType objects.
   • An AndAggregatedType object and a ClauseType object.
   • An OrAggregatedType object and a ClauseType object.
   
   

   Each ClauseType object contains three elements:

   • Modifier: It is a string with the modifier used. This information is optional but we can select any of these modifiers:
     • above: The hedge above identifies the first point on x-axis, named x_max, at which the term is a characterized by the maximum degree value: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)=\left\{\begin{array}{l}0\mathrm{ if\; x}<x_{\max }\\ 1-\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\mathrm{ if\; x}\ge \; <!--greater-than\; or\; equal\; to-->x_{\max }\end{array}\right.}$
     • any: Hedge any: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)=1}$
     • below: The hedge below identifies the first point on x-axis, named x_max, at which the term is a characterized by the maximum degree value: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)=\left\{\begin{array}{l}0\mathrm{ if\; x}>x_{\max }\\ 1-\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\mathrm{ if\; x}\le \; <!--less-than\; or\; equal\; to-->x_{\max }\end{array}\right.}$
     • extremely: Hedge extremely: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)={\left(\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\right)}^3}$
     • intensify: Hedge intesify: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)=\left\{\begin{array}{l}2·\; <!--middle\; dot-->{\left(\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\right)}^2\mathrm{ if }0\le \; <!--less-than\; or\; equal\; to-->\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\le \; <!--less-than\; or\; equal\; to-->0.5\\ 1-2·\; <!--middle\; dot-->{\left(1-\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\right)}^2\mathrm{ if }\mathrm{0.5}\le \; <!--less-than\; or\; equal\; to-->\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\le \; <!--less-than\; or\; equal\; to-->1.0\end{array}\right.}$
     • more_or_less: Hedge more or less: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)={\left(\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\right)}^{\frac{1}{3}}}$
     • norm: Hedge norm where x_max is the maximum membership degree of the function: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)=\frac{\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)}{{\mathrm{\mu \; <!--micro\; sign-->}}_{\max }}}$
     • not: Hedge not: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)=1-\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)}$
     • plus: Hedge plus: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)={\left(\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\right)}^{\frac{5}{4}}}$
     • seldom: Hedge seldom: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_n\left(x\right)=\left\{\begin{array}{l}\sqrt{\frac{\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)}{2}}\mathrm{ if }0\le \; <!--less-than\; or\; equal\; to-->\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\le \; <!--less-than\; or\; equal\; to-->0.5\\ \sqrt{\frac{1-\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)}{2}}\mathrm{ if }0.5<\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\le \; <!--less-than\; or\; equal\; to-->1\end{array}\right.}$
     • slightly: Hedge slightly: μ_M(x) = intensify [norm (plus μ(x) AND not very μ(x))]
     • somewhat: Hedge somewhat: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)={\left(\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\right)}^{\frac{1}{2}}}$
     • very: Hedge very: ${\displaystyle {\mathrm{\mu \; <!--micro\; sign-->}}_M\left(x\right)={\left(\mathrm{\mu \; <!--micro\; sign-->}\left(x\right)\right)}^2}$
     • custom_\S*: A custom hedge
     
     
   • An FuzzyVariableType object.
   • An FuzzyTermType object.

   In order to illustrate this type of variable, let us allow to consider that our knowledge base has two fuzzy variables (food and service) with three terms (low, middle, high). We can create the next terms for the new variable "aggregated":

           AggregatedFuzzyTermType term1 = new AggregatedFuzzyTermType ("bad", new AndAggregatedType(new ClauseType (food, (FuzzyTerm) food.getTerm("low")), new ClauseType (service, (FuzzyTerm) food.getTerm("low"))));
           AggregatedFuzzyTermType term2 = new AggregatedFuzzyTermType ("good", new AndAggregatedType(new ClauseType (food, (FuzzyTerm) food.getTerm("high")), new ClauseType (service, (FuzzyTerm) food.getTerm("high"))));
   
           aggregated.addAggregatedFuzzyTerm(term1);
           aggregated.addAggregatedFuzzyTerm(term2);
           

3. TsukamotoTermType: It represents an output fuzzy variable that can be used in rule bases of Tsukamoto systems. Each object of this class contains the following information:
   
   • Name: It is a string with a unique name for the fuzzy variable. This information is required when we create the variable.
   • Scale: It is a string with the scale used to measure a fuzzy variable. This information is optional when we create the variable.
   • DomainLeft: It is a float that represents the left boundary of the universe of discourse of a fuzzy variable. This information is required when we create the variable.
   • DomainRight: It is a float that represents the right boundary of the universe of discourse of a fuzzy variable. This information is required when we create the variable.
   • Type: It is a string with the position of a fuzzy variable in a rule (consequent part or antecedent part). Its values should be "output". This information is optional when we create the variable due to that its default value is "output" when we do not indicate any value.
   • Combination: It is a string with the aggregation method used when this variable is involved in the consequent part of the rules. This information is optional when we create the variable. Its default value is "WA" but we can select any of these aggregation methods:
     
     • WA: The weighted average
     • custom_\S*: A custom aggregation method
     
     
   • DefaultValue: It is a float value used only when no rule has fired for the variable at issue. This information is optional when we create the variable. Its default value is 0.
   • NetworkAddress: It is a string with the location of the fuzzy variable in a computer network. This information is optional when we create the variable. Its default value is "127.0.0.1".
   
   

   Next Java code creates an input fuzzy variable with the name "tip", the left boundary 0, right boundary 20, and the default values of the rest of attributes. Moreover, this variable is added to the knowledge base of our fuzzy system:

   TsukamotoVariableType tip = new TsukamotoVariableType("tip", 0, 20);
   kb.addVariable(tip);
           

   Then, we define the monotone linguistic terms of the variable. Each term contains the attributes: name (string), complement (string "true" or "false"), the type of membership function, and a float list with the parameters required for the corresponding fuzzy set. The attribute complement is optional and its default value is "false". We can use the following monotone membership functions:

   • Left Linear: This option defines the left linear function depending on two parameters a and b. Next Java code generates a term of this function with the name "cheap", a=0, b=10, and add it to the variable "tip":
     
     

     TsukamotoTermType cheap = new TsukamotoTermType("cheap", FuzzyTermType.TYPE_leftLinearShape,(new float[] {0f, 10f}));
     tip.addTsukamotoTerm(cheap);
                 

     
   • Right Linear: This option defines the right linear function depending on two parameters a and b. Next Java code generates a term of this function with the name "generous", a=15, b=20, and add it to the variable "tip":
     
     

     TsukamotoTermType generous = new TsukamotoTermType("generous", FuzzyTermType.TYPE_rightLinearShape,(new float[] {15f, 20f}));
     tip.addTsukamotoTerm(generous);
                 

     
   • Left Gaussian: This option defines the left Gaussian function depending on two parameters c and σ. Next Java code generates a term of this function with the name "cheap", c=5, σ=2, and add it to the variable "tip":
     
     

     TsukamotoTermType cheap = new TsukamotoTermType("cheap", FuzzyTermType.TYPE_leftGaussianShape,(new float[] {5f, 2f}));
     tip.addTsukamotoTerm(cheap);
                 

     
   • Right Gaussian: This option defines the right Gaussian function depending on two parameters c and σ. Next Java code generates a term of this function with the name "generous", c=18, σ=2, and add it to the variable "tip":
     
     

     TsukamotoTermType generous = new TsukamotoTermType("generous", FuzzyTermType.TYPE_rightGaussianShape,(new float[] {18f, 2f}));
     tip.addTsukamotoTerm(generous);
                 

     
   • Z-Shape: This spline-based curve is so named because of its Z-shape and it depends on two parameters a, and b. Next Java code generates a term of this function with the name "cheap", a=5, b=10, and add it to the variable "tip":
     
     

     TsukamotoTermType cheap = new TsukamotoTermType("cheap", FuzzyTermType.TYPE_zShape,(new float[] {5f, 10f}));
     tip.addTsukamotoTerm(cheap);
                 

     
   • S-Shape: This spline-based curve is so named because of its S-shape and it depends on two parameters a, and b. Next Java code generates a term of this function with the name "generous", a=15, b=18, and add it to the variable "tip":
     
     

     TsukamotoTermType generous = new TsukamotoTermType("generous", FuzzyTermType.TYPE_sShape,(new float[] {15f, 18f}));
     tip.addTsukamotoTerm(generous);
                 

     
   • PointSetMonotonic Shape: This option defines a function by using a set of points defined by the user (monotonic piece-wise function). This function has an additional attribute (interpolationMethod) and the list of parameters is a list of pointType objects defined by the user:
     • interpolationMethod: It defines the method to interpolate the points defined by the user. This attribute can table the following values: "linear" for implementing the Linear interpolation; "cubic" for implementing the monotone cubic interpolation. This attribute is optional and its default value is "linear".

     Next Java code generates a term of this function with the name "generous", the method to interpolate by default, and a list with the point (15, 0), (17, 0.5) and (19, 1).

     List points = new ArrayList();
     points.add(new PointType(15f, 0f));
     points.add(new PointType(17f, 0.5f));
     points.add(new PointType(19f, 1f));
     
     TsukamotoTermType generous = new TsukamotoTermType("generous", FuzzyTermType.TYPE_pointSetMonotonicShape, points);
     tip.addTsukamotoTerm(generous);
                 

     
   • Custom Membership Function: A custom monotone function implemented by the users


4. TskVariableType: It represents an output fuzzy variable that can be used in rule bases of TSK systems. Each object of this class contains the following information:
   
   
   • Name: It is a string with a unique name for the fuzzy variable. This information is required when we create the variable.
   • Scale: It is a string with the scale used to measure a fuzzy variable. This information is optional when we create the variable.
   • Type: It is a string with the position of a fuzzy variable in a rule (consequent part or antecedent part). Its values should be "output" in this type of variables. This information is optional when we create the variable due to that its default value is "output".
   • Combination: It is a string with the aggregation method used when this variable is involved in the consequent part of the rules. This information is optional when we create the variable. Its default value is "WA" but we can select any of these aggregation methods:
     
     
     • WA: The weighted average
     • custom_\S*: A custom aggregation method
     
     
   • DefaultValue: It is a float value used only when no rule has fired for the variable at issue. This information is optional when we create the variable. Its default value is 0.
   • NetworkAddress: It is a string with the location of the fuzzy variable in a computer network. This information is optional when we create the variable. Its default value is "127.0.0.1".
   
   

   Next Java code creates a tsk variable with the name "tip", the left boundary 0, right boundary 20, and the default values of the rest of attributes. Moreover, this variable is added to the knowledge base of our fuzzy system:

   TskVariableType tip = new TskVariableType("tip", 0, 20);
   kb.addVariable(tip);
           

   Then, we define the linguistic terms of the variable. Each term contains the attributes: name (string), order (an int value 0 or 1), and a float list with the parameters required for the polynomial. The attribute order describes the order of a TSK system. Notice that when the order is 1, the first value of the list is the independent term of the polynomial, and the rest of weights are assigned following the order of the variables in the knowledge base. In order to show a simple example, let us to consider that our knowledge base has two input variables (food and service). We can define the next two terms with the orders 0 and 1:

   TskTermType average = new TskTermType("average", 0, (new float[] { 10.5f})); // y = 10.5
   TskTermType cheap = new TskTermType("cheap", 1, (new float[] { 1.5f, 5.6f, 6.0f })); // y = 1.5 + 5.6 * food + 6.0 * service
   tip.addTskTerm(average); tip.addTskTerm(cheap);
           



5. AnYaDataCloudType: It represents a data cloud that can be involved in the antecedent part of the rules in AnYa systems. Each object of this class contains the following information:
   
   
   • Name: It is a string with a unique name for the fuzzy variable. This information is required when we create the variable.
   • NetworkAddress: It is a string with the location of the fuzzy variable in a computer network. This information is optional when we create the variable. Its default value is "127.0.0.1".

   Next Java code creates a AnYa variable with the name "foodRancidServicePoor" and the default value of the attribute NetworkAddress. Moreover, this variable is added to the knowledge base of our fuzzy system:

   AnYaDataCloudType foodRancidServicePoor = new AnYaDataCloudType("foodRancidServicePoor");
   kb.addVariable(foodRancidServicePoor);
           

   Each object of this class also contains a list of float values that represents the datums in the cloud. Next Java code add the list of datums to the variable "food":

   foodRancidServicePoor.setTerms((new float[] { 0.5f, 1.0f }));
           

Rule Base

The objects of the classes MamdaniRuleBase, TsukamotoRuleBase, TskRuleBase, and/or AnYaRuleBase, represent fuzzy rule sets for Mamdani, Tsukamoto, TSK, and anYa fuzzy systems, respectively. A FuzzyInferenceSystem object contains one or multiple MamdaniRuleBase, TsukamotoRulBase, TskRuleBase, and/or AnYaRuleBase objects in order to describe different behaviors of the system, being evaluated in the order in which they have been added to the FuzzyInferenceSystem object. Thus, we have to create the objects MamdaniRuleBaseType, TsukamotoRuleBaseType, TskRuleBaseType, and AnYaRuleBaseType, that we want to include in our fuzzy system and then we add them to our fuzzy system:

MamdaniRuleBaseType rbMam = new MamdaniRuleBaseType("MamdaniRB1");
tipper.addRuleBase(rbMam);

TsukamotoRuleBaseType rbTsu = new TsukamotoRuleBaseType("TsukamotoRB1");
tipper.addRuleBase(rbTsu);

TskRuleBaseType rbTsk = new TskRuleBaseType("TSKRB1");
tipper.addRuleBase(rbTsk);

AnYaRuleBaseType rbAnY = new AnYaRuleBaseType("AnYaRB1");
tipper.addRuleBase(rbAnY);
 

The objects mamdaniRuleBase, tsukamotoRuleBase, and tskRuleBase have five attributes:

• Name: It is a string with a unique name for the rule base. This information is required when we create the rule base.
• activationMethod: It is a string with the implication method used. This information is optional and its default value is MIN, but we can select any of these implication methods:
  • MIN: Operator minimum
  • PROD: Operator product
  • BDIF: Bounded difference
  • DRP: Drastic product
  • EPROD: Einstein product
  • HPROD: Hamacher product
  • NILMIN: Nilpotent minimum
  • custom_\S*: A custom method
  
  
• andMethod: It is a string which indicates the and algorithm used in all the rules included in the rule base. This information is optional and its default value is MIN, but we can select any of these implication methods:
  • MIN: Operator minimum
  • PROD: Operator product
  • BDIF: Bounded difference
  • DRP: Drastic product
  • EPROD: Einstein product
  • HPROD: Hamacher product
  • NILMIN: Nilpotent minimum
  • custom_\S*: A custom method
  
  
• orMethod: It is a string which indicates the or algorithm used in all the rules included in the rule base. This information is optional and its default value is MAX, but we can select any of these implication methods:
  • MAX: Operator maximum
  • PROBOR: Probabilistic sum
  • BSUM: Bounded sum
  • DRS: Drastic sum
  • ESUM: Einstein sum
  • HSUM: Hamacher sum
  • NILMAX: Nilpotent maximum
  • custom_\S*: A custom method
  
  
• NetworkAddress: It is a string with the location of the fuzzy variable in a computer network. This information is optional when we create the variable. Its default value is "127.0.0.1".

The objects AnYaRuleBase have three attributes:

• Name: It is a string with a unique name for the rule base. This information is required when we create the rule base.
• activationMethod: It is a string with the implication method used. This information is optional and its default value is MIN, but we can select any of these implication methods:
  • MIN: Operator minimum
  • PROD: Operator product
  • BDIF: Bounded difference
  • DRP: Drastic product
  • EPROD: Einstein product
  • HPROD: Hamacher product
  • NILMIN: Nilpotent minimum
  • custom_\S*: A custom method
  
  
• NetworkAddress: It is a string with the location of the fuzzy variable in a computer network. This information is optional and its default value is "127.0.0.1".

The MamdaniRuleBase and TsukamotoRuleBase objects contain a list of FuzzyRuleType objects. The tskRuleBase objects contain a list of TskFuzzyRuleType objects. The AnYaRuleBase objects contain a list of AnYaRuleType objects. In the following, we will explain each type of rule.

FuzzyRuleType

The FuzzyRuleType objects represent Mamdani and Tsukamoto rules with the form IF-THEN-ELSE. Each rule has 6 attributes:

• Name: It is a string with a unique name for the rule. This information is required when we create the rule.
• Connector: It is a string which indicates the logical operator used to connect the involved clauses in the antecedent part. Its default value is and but we can select any of these options: and, AND, or, OR.
• andMethod: It is a string that indicates the and algorithm used for this rule if the chosen connector is and. This information is optionaland and its default value is the MIN operator selected when we have defined the MamdaniRuleBase or TsukamotoRuleBase object, but we can select any of these implication methods for this rule:
  • MIN: Operator minimum
  • PROD: Operator product
  • BDIF: Bounded difference
  • DRP: Drastic product
  • EPROD: Einstein product
  • HPROD: Hamacher product
  • NILMIN: Nilpotent minimum
  • custom_\S*: A custom method
  
  
• orMethod: It is a string that indicates the or algorithm used for this rule if the chosen connector is or. This information is optional and its default value is the MAX operator selected when we have defined the MamdaniRuleBase or TsukamotoRuleBase object, but we can select any of these implication methods for this rule:
  • MAX: Operator maximum
  • PROBOR: Probabilistic sum
  • BSUM: Bounded sum
  • DRS: Drastic sum
  • ESUM: Einstein sum
  • HSUM: Hamacher sum
  • NILMAX: Nilpotent maximum
  • custom_\S*: A custom method
  
  
• Weight: It is a float value that represents the importance of the rule to be used by the inference engine. This information is optional, its domain is [0, 1] and its default value is 1.0.
• NetworkAddress: It is a string with the location of the rule in a computer network. This information is optional when we create the rule. Its default value is "127.0.0.1".

For instance, the definition of a simple rule is as follow:

FuzzyRuleType rule1 = new FuzzyRuleType("rule1", "or", "MAX", 1.0f);

Each FuzzyRuleType object consists of one AntecedentType object and one ConsequentType object. The AntecedentType objects contain a list of ClauseType objects that represent Mamdani clauses involved in the antecedent part. The ConsequentType objects contain one ClauseType object for the part then, and one optional ClauseType object for the else part. Each ClauseType object has an attribute modifier, a FuzzyVariableType object and a FuzzyTermType object. Notice that, Tsukamoto rules can only contain monotone variables in the definition ClauseType objects for the consequent part of the rule. The attribute modifier of the ClauseType describes a modification to the linguistic term used in the clause. This information is optional and we can select any of these modifiers:

• above
• any
• below
• extremely
• intensify
• more_or_less
• norm
• not
• plus
• seldom
• slightly
• somewhat
• very
• custom_\S* for a custom hedge.

Thus, we can define the antecedent and consequent of the rule as follow:

FuzzyRuleType rule1 = new FuzzyRuleType("rule1", "or", "MAX", 1.0f);

AntecedentType ant1 = new AntecedentType();
ant1.addClause(new ClauseType(food, rancid));
ant1.addClause(new ClauseType(service, poor, "very"));
rule1.setAntecedent(ant1);

ConsequentType con1 = new ConsequentType();
con1.addThenClause(tip, cheap);
rule1.setConsequent(con1);

rbMam.addRule(rule1);

TskFuzzyRuleType

The TskFuzzyRuleType objects represent TSK rules with the form IF-THEN-ELSE. Each rule has 6 attributes:

• Name: It is a string with a unique name for the rule. This information is required when we create the rule.
• Connector: It is a string which indicates the logical operator used to connect the involved clauses in the antecedent part. Its default value is and but we can select any of these options: and, AND, or, OR.
• andMethod: It is a string that indicates the and algorithm used for this rule if the chosen connector is and. This information is optional and its default value is the MIN operator selected when we have defined the MamdaniRuleBase or TsukamotoRuleBase object, but we can select any of these implication methods for this rule:
  • MIN: Operator minimum
  • PROD: Operator product
  • BDIF: Bounded difference
  • DRP: Drastic product
  • EPROD: Einstein product
  • HPROD: Hamacher product
  • NILMIN: Nilpotent minimum
  • custom_\S*: A custom method
  
  
• orMethod: It is a string that indicates the or algorithm used for this rule if the chosen connector is or. This information is optional and its default value is the MAX operator selected when we have defined the MamdaniRuleBase or TsukamotoRuleBase object, but we can select any of these implication methods for this rule:
  • MAX: Operator maximum
  • PROBOR: Probabilistic sum
  • BSUM: Bounded sum
  • DRS: Drastic sum
  • ESUM: Einstein sum
  • HSUM: Hamacher sum
  • NILMAX: Nilpotent maximum
  • custom_\S*: A custom method
  
  
• Weight: It is a float value that represents the importance of the rule to be used by the inference engine. This information is optional, its domain is [0, 1] and its default value is 1.0.
• NetworkAddress: It is a string with the location of the rule in a computer network. This information is optional when we create the rule. Its default value is "127.0.0.1".

For instance, the definition of a simple rule is as follow:

TskFuzzyRuleType rule1 = new TskFuzzyRuleType("rule1", "or", "MAX", 1.0f);

Each TskFuzzyRuleType object consists of one AntecedentType object and one TskConsequentType object. The AntecedentType objects contain a list of ClauseType objects that represent Mamdani clauses involved in the antecedent part. The TskConsequentType objects contain one TskClauseType object (another one if we use the else part of the rule), which represent the THEN[-ELSE] part of a rule in a TSK system (constant or linear function). Each ClauseType object has an attribute modifier, a FuzzyVariableType object and FuzzyTermType object. Each TskClauseType object has a TskVariableType object and a TskTermType object.

Thus, we can definde the antecedent and consequent of the rule as follow:

TskFuzzyRuleType rule1 = new TskFuzzyRuleType("rule1", "or", "MAX", 1.0f);

AntecedentType ant1 = new AntecedentType();
ant1.addClause(new ClauseType(food, rancid));
ant1.addClause(new ClauseType(service, poor));
rule1.setAntecedent(ant1);

TskConsequentType con1 = new TskConsequentType();
con1.addTskThenClause(tip, cheap);
rule1.setTskConsequent(con1);

rbTsk.addTskRule(rule1);

AnYaRuleType

The AnYaRuleType objects represent AnYa rules with the form IF-THEN-ELSE. Each rule has 3 attributes:

• Name: It is a string with a unique name for the rule. This information is required when we create the rule.
• Weight: It is a float value that represents the importance of the rule to be used by the inference engine. This information is optional, its domain is [0, 1] and its default value is 1.0.
• NetworkAddress: It is a string with the location of the rule in a computer network. This information is optional when we create the rule. Its default value is "127.0.0.1".

For instance, the definition of a simple rule is as follow:

AnYaRuleType rule1 = new AnYaRuleType("rule1");

Each AnYaRuleType object consists of one AnYaAntecedentType object and one ConsequentType object or TskConsequentType object. The AnYaAntecedentType objects represents the antecedent part of a rule based on data clouds and each one contains one AnYaDataCloudType object that represents the data cloud to be used in the rule. Thus, we can define the antecedent and consequent of the rule as follow:

AnYaRuleType rule1 = new AnYaRuleType("rule1");

AnYaAntecedentType ant1 = new AnYaAntecedentType();
ant1.setDataCloudName(foodRancidServicePoor);
rule1.setAnYaAntecedent(ant1);

ConsequentType con1 = new ConsequentType();
con1.addThenClause(tip, cheap);
rule1.setConsequent(con1);

rbAnY.addRule(rule1);

Load/Write FML Files

We can load and write fuzzy systems according to the IEEE standard. JFML makes use of the new Java API JAXB (Java Architecture for XML Binding), which provides a fast and convenient way to bind XML schemas and Java representations, making it easy for Java developers to incorporate XML data and processing functions in Java applications.

You can read (unmarshalling) a XML file according to the IEEE standard with JFML using the next Java code:

    File xml = new File("./XMLFiles/tipper.xml");
    FuzzyInferenceSystem tipper = JFML.load(xml);
    

    File xml = new File("./XMLFiles/ourFS.xml");
    JFML.writeFSTtoXML(fs, xml);
    

Notice that FML code can be executed by considering two different approaches: a XSLT-based translation of FML programs, and a Java-based execution of FML code. In the first case, an XSLT engine translates an FML code into a Java program describing fuzzy systems by means of a pure textual manipulation of the FML description of the systems. In the second case, a Java method has been opportunely designed to read the FML code and automatically build a hierarchy of Java objects describing the related fuzzy systems. In terms of development effort between these two approaches for developing fuzzy inference systems, the second approach appears to be more convenient to use than the first one. Indeed, in the first case, a programmer needs first to apply the XSLT engine and thus generating the related Java code, then compiling the Java code to produce a Java bytecode ready to interpret and to run. In the second case, it is sufficient for a programmer to load the FML code in his/her Java application, thus automatically obtaining a collection of Java objects ready to use with the Java-based fuzzy inference engine in order to effectively run the designed fuzzy system.

    ImportFCL fcl = new ImportFCL();
    FuzzyInferenceSystem fs = fcl.importFuzzySystem("./XMLFiles/robot.fcl");
    

    ImportMatlab fis = new ImportMatlab();
    FuzzyInferenceSystem fs = fis.importFuzzySystem("./XMLFiles/IrisMamdani1.fis");
    

    ImportPMML pmml    = new ImportPMML();
    FuzzyInferenceSystem fs = pmml.importFuzzySystem("./XMLFiles/TipperTSK.frbsPMML");
    

Similarly, we can export a FLS designed with JFML to other formats. For example, next Java code shows an example of writing a FLS object (fs) to FCL:

    ExportFCL fcl = new ExportFCL();
    fcl.exportFuzzySystem(fs, "./XMLFiles/robot.fcl");
    

    ExportMatlab fis = new ExportMatlab();
    fis.exportFuzzySystem(fs, "./XMLFiles/IrisMamdani1.fis");
    

    ExportPMML pmml = new ExportPMML();
    pmml.exportFuzzySystem(fs, "./XMLFiles/TipperTSK.frbsPMML");
    

Fuzzy Inference

    public class EvaluateTipperExample {
        public static void main(String[] args) {
            // Loading Fuzzy System from an XML file according the standard IEEE 1855
            File xml = new File("./XMLFiles/tipper.xml");
            FuzzyInferenceSystem tipper = JFML.load(xml);
                
            // Set inputs values
            KnowledgeBaseVariable food =  fs.getVariable("food");
            KnowledgeBaseVariable service =  fs.getVariable("service");
            food.setValue(6);
            service.setValue(8);
            
            // Fuzzy inference
            tipper.evaluate();	
            
            // Get output
            KnowledgeBaseVariable tip =  fs.getVariable("tip");
            float value = tip.getValue();
            
            // Printing results
            System.out.println("RESULTS");
            System.out.println(" (INPUT): " + food.getName() + "=" + food.getValue() + ", " + service.getName() + "=" + service.getValue());
            System.out.println(" (OUTPUT): " + tip.getName() + "=" + value);
            
            
            // Printing the FuzzySystem
            System.out.println(fs.toString());
        }
    }
    

Moreover, this Java code also prints the definition of the fuzzy system (Knowledge base + Rule bases) making use of the method toString of the FuzzyInferenceSystem class. Notice that the method toString is available in most of the classes of JFML.

Extensibility

The modular design of JFML allows us to extend the API easily. Moreover, we can add new elements making use of the custom elements that have the classes, according to the pattern [custom_\S*]. This extension mechanism allows to define new elements without changing the language grammar.

For instance, if we want to introduce a new T-norm in JFML (i.e., the T-norm TN), we must include the following changes in the AndLogicalType class:

• Include in the method "operate" the option for the new T-norm:

  public float operate(float x, float y) {
  	String op = getOperator();
  	if (op.equals(StandardAndMethodType.MIN.value()))
  		return min(x, y);
  	else if (op.equals(StandardAndMethodType.PROD.value()))
  		return prod(x, y);
  	else if (op.equals(StandardAndMethodType.BDIF.value()))
  		return bdif(x, y);
  	else if (op.equals(StandardAndMethodType.DRP.value()))
  		return drp(x, y);
  	else if (op.equals(StandardAndMethodType.EPROD.value()))
  		return eprod(x, y);
  	else if (op.equals(StandardAndMethodType.HPROD.value()))
  		return hprod(x, y);
  	else if (op.equals(StandardAndMethodType.NILMIN.value()))
  		return nilmin(x, y);
  	else if (op.equals("custom_TN"))
  		return custom_TN(x, y);
  	else
  		return min(x, y); 
  }
  			

• Add the method custom_TN to the class, which implements the T-norm TN:
  

  private float custom_TN(float x, float y) { 
  	// TODO 
  }
  			

Now, we could use the T-norm custom_TN in the definitions of our fuzzy systems according to the IEEE standard. On the other hand, The modular design allows us to easily extend JFML with new functions. For instance, JMFL includes the class ImportFCL that allows us to import FCL fuzzy systems.

With the aim of having a code free of bugs we recommend running unit tests when coding new functions for JFML. In short, unit testing consists of writing short code fragments which are aimed at testing that the new function works properly.

Once JFML is extended, it is mandatory to check not only that the new funcitons work properly but also that everything is still in accordance with the IEEE Std 1855. With that aim, we recommend running the provided examples.

Embedded Systems

The embedded system module assists developers in the design and implementation of fuzzy systems for open hardware embedded systems. The JFML is now ready for Arduino and Raspberry Pi with this module, but it can be easily extended to other hardware architectures. Moreover, the module supports several connection types (WiFi, Bluetooth and USB) in order to make feasible running fuzzy systems in a remote computer when, due to hardware limitations, it is not possible to run the fuzzy systems locally in the embedded systems. In addition, the module allows to automatically generate runnable files on Arduino or Raspberry Pi in order to support non-expert users, i.e., users without specific knowledge about embedded systems or without strong programming skills.

The main class is EmbeddedSystem wich is responsible for defining both the characteristics and the type of connection with the embedded system. It requires a name, a type of connection (WiFi, Bluetooth and USB) and a baud rate for establishing the connection with the JFML core. It has also associated a list of EmbeddedVariable objects which are in charge of the association between variables of the knowledge base and sensors/actuators.
The classes EmbeddedSystemArduino and EmbeddedSystemRaspberry, which extend the abstract class EmbeddedSystem, are used for Arduino-based and RaspberryPi-based implementations. Arduino boards can be connected to serial ports (USB or Bluetooth) or WiFi and used for designing FLCs in a simple way. These different connections are taken into account by the EmbeddedSystemArduinoUSB, EmbeddedSystemArduinoBluetooth or EmbeddedSystemArduinoWIFI classes which extend the EmbeddedSystemArduino class. Similarly, the classes EmbeddedSystemRaspberryUSB, EmbeddedSystemRaspberryBluetooth or EmbeddedSystemRasperryWIFI, which extend the EmbeddedSystemRaspberry class, are in charge of defining the different connections between the Raspberry Pi and the JFML.

For instance, if we want to create an Arduino-based embedded system connected via USB with 2 sensors, we can do it as follow:

• Associating variables from the knowledge base to the sensors. For example, a ultrasonic HCSR04 sensor and a LED:
  

  Sensor sensor1 = new ArduinoHC_SR04("name_sensor", ArduinoPin.PIN_1, ArduinoPin.PIN_2);
  Sensor sensor2 = new ArduinoLED("name_sensor", ArduinoPin.PIN_3);
  
  ArrayList embeddedVariables = new ArrayList<>();
  embeddedVariables.add(new EmbeddedVariableArduino(0,variable1,sensor1));
  embeddedVariables.add(new EmbeddedVariableArduino(1,variable2,sensor2));
  			

• Creating an embedded system instance of Arduino with the sensors defined bellow and connected via USB to 9600 baud rate:

  EmbeddedSystem arduinoUSB;
  arduinoUSB = new EmbeddedSystemArduinoUSB ("name_embedded","USB_PORT", 9600, embeddedVariables); 
              

Or, for example, if we want to create a RaspberryPi-based embedded system connected via WiFi with a DHT22 temperature sensor, we can do it as follow:

• Associating variables from the knowledge base to the sensors. For example, a ultrasonic HCSR04 sensor and a LED:
  

  Sensor sensor1 = new RaspberryDHT22("name_sensor", RaspberryPin.PIN_1, RaspberryPin.PIN_2);
  
  ArrayList embeddedVariables = new ArrayList<>();
  embeddedVariables.add(new EmbeddedVariableArduino(0,variable1,sensor1));
  			

• Creating an embedded system instance of RaspberryPi with the DHT22 sensor defined bellow and connected via WiFi:

  EmbeddedSystem rpiWIFI;
  rpiWIFI = new EmbeddedSystemRasperryWIFI ("name_embedded","IP_ADDRESS", "SSID", "PASSWORD", embeddedVariables); 
              

Now, we can run an instanceof a FLS on the arduino board and/or the RaspberryPi iteratively or during a single iteration. The EmbeddedController class is in charge of coordinating all the embedded systems connected to the JFML. As many embedded systems as the designer desires could be included in a unique EmbeddedController instance. For example, if we want to run a FLS indefinitely on the two embedded systems created before, we have to do the following:

ArrayList boards = new ArrayList<>();
boards.add(arduinoUSB);
boards.add(rpiWIFI);

EmbeddedController controller = new EmbeddedControllerSystem(boards, FLS);
controller.run();
    

Once a embedded system instance is created in JFML, a runnable file according to the architecture design requirements of the embedded system is necessary. The EmbeddedSystem class defines an abstract method to create automatically this file where a user without specific knowledge about the embedded system architecture or programming language could easily run a FLC on it. For example, to create a runnable file for the previously defined Arduino board, we can do it as follow:

arduinoUSB.createRunnableEmbeddedFile("name_file");
    

Sensors

• Temperature DHT22 sensor: default constructor
  

  Sensor sensorArduino = new ArduinoDHT22_temperature("name", ArduinoPin.PIN_XX); 
  Sensor sensorRaspberry = new RaspberryDHT22_temperature("name", RaspberryPin.GPIOXX);  
          

• Humidity DHT22 sensor: default constructor
  

  Sensor sensorArduino = new ArduinoDHT22_humidity("name", ArduinoPin.PIN_XX); 
  Sensor sensorRaspberry = new RaspberryDHT22_humidity("name", RaspberryPin.GPIOXX);  
          

• Ultrasonic HC_SR04 sensor: default constructor
  

  Sensor sensorArduino = new ArduinoHC_SR04("name", ArduinoPin.PIN_XX, ArduinoPin.PIN_XX); 
  Sensor sensorRaspberry = new RaspberryHC_SR04("name", RaspberryPin.GPIOXX, RaspberryPin.GPIOXX);  
          

• Motion HC_SR501 sensor: default constructor
  

  Sensor sensorArduino = new ArduinoHC_SR501("name", ArduinoPin.PIN_XX, timeout); 
  Sensor sensorRaspberry = new RaspberryHC_SR501("name", RaspberryPin.GPIOXX, timeout);  
          

• Light LDR sensor: default constructor
  

  Sensor sensorArduino = new ArduinoLIGHT("name", ArduinoPin.PIN_XX); 
  Sensor sensorRaspberry = new RaspberryLIGHT("name", RaspberryPin.GPIOXX);  
          

• LED PWM sensor: default constructor
  

  Sensor sensorArduino = new ArduinoLED_PWM("name", ArduinoPin.PIN_XX); 
  Sensor sensorRaspberry = new RaspberryLED_PWM("name", RaspberryPin.GPIOXX);  
          

• Controller motor L298N actuator: default constructor
  

  Sensor actuatorArduino = new ArduinoH_BRIDGE_L298N(String name, ArduinoPin ENA, ArduinoPin IN1, ArduinoPin IN2, ArduinoPin IN3, ArduinoPin IN4, ArduinoPin ENB, int min, int max, int minSpeed, int maxSpeed);
  Sensor actuatorRaspberry = new ArduinoH_BRIDGE_L298N(String name, ArduinoPin ENA, ArduinoPin IN1, ArduinoPin IN2, ArduinoPin IN3, ArduinoPin IN4, ArduinoPin ENB, int min, int max, int minSpeed, int maxSpeed);  
          

• DC motor actuator: default constructor
  

  Sensor actuatorArduino = new ArduinoDCMOTOR_PWM("name", ArduinoPin.PIN_XX); 
  Sensor actuatorRaspberry = new RaspberryDCMOTOR_PWM("name", RaspberryPin.GPIOXX);  
          

• Servo SG90 actuator: default constructor
  

  Sensor actuatorArduino = new ArduinoSERVO("name", ArduinoPin.PIN_XX); 
  Sensor actuatorRaspberry = new RaspberrySERVO("name", RaspberryPin.GPIOXX);  
          

Several real word problems can be found in the Examples. section.

Command line

The JFML library can be freely downloaded from GitHub. A folder with a runnable version of the JFML Library (compiled with JRE v8) and several XML files as examples can be found in the Examples folder.

The JFML library can be run with 3 main arguments (ProblemName InferenceExample DataFile) but brackets are not required (in JFML-vx.x.jar, x corresponds with the version of the library):

    Usage: java -jar JFML-vx.x.jar [options]
        Options: Tipper [Mamdani1 | Mamdani2 | Mamdani3 | TSK | Tsukamoto1 | Tsukamoto2 | AnYa] test-data-file
        Options: JapaneseDietAssessment Mamdani test-data-file
        Options: Iris [Mamdani1 | Mamdani2 | Mamdani3] test-data-file
        Options: InvertedPendulum [Mamdani1 | Mamdani2 | TSK1 | TSK2] test-data-file
        Options: Robot Mamdani test-data-file

    You can also run the library with a specific instance as follows:
        Options: ProblemName InferenceExample V1 D1 V2 D2 ... 
        ProblemName: Tipper, JapaneseDietAssessment, etc.
        InferenceExample; Mamdani, Mamdani1, Mamdani2, TSK, AnYa, etc.
    

Notice that the combination of ProblemName and InferenceExample must be in accordance with the name of an XML file in the folder ./XMLFiles. You must be also sure of providing the entire list of pairs variable name (Vi, as it is in the XML file) and numerical value (Di) for evaluation.

Example:

java -jar ./lib/JFML-vx.x.jar Iris Mamdani2 SepalLength 5.1 SepalWidth 3.5 PetalLength 1.4 PetalWidth 0.2

You can also run the library with a specific instance, for your own XML file, considering the options: XMLfilePath NbOutputs ON1 ON2 ... V1 D1 V2 D2 ...

Example:

java -jar ./lib/JFML-vx.x.jar ./XMLFiles/RobotIEEEstd1855.xml 2 la av rd 0.2 dq 0.25 o 20 v 0.25
  

Running the examples

Before running the examples, please be sure the XMLFiles folder contains the required XML files. Otherwise, you can create some of them from the command line:
Examples:

    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateIrisMamdaniExampleXML1
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateIrisMamdaniExampleXML2
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateIrisMamdaniExampleXML3
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateInvertedPendulumMamdaniExampleXML1
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateInvertedPendulumMamdaniExampleXML2
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateInvertedPendulumTSKExampleXML1
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateInvertedPendulumTSKExampleXML2
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateJapaneseDietAssessmentMamdaniExampleXML
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateTipperMamdaniExampleXML1
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateTipperMamdaniExampleXML2
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateTipperMamdaniExampleXML3
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateTipperTSKExampleXML
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateTipperTsukamotoExampleXML1
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateTipperTsukamotoExampleXML2
    java -classpath ./lib/JFML-vx.x.jar jfml.test.CreateTipperAnYaExampleXML
    

Test:

    java -jar ./lib/JFML-vx.x.jar Iris Mamdani1 ./XMLFiles/test-data-Iris1.txt
    java -jar ./lib/JFML-vx.x.jar Iris Mamdani1 PetalWidth 0.2
    java -jar ./lib/JFML-vx.x.jar Iris Mamdani2 ./XMLFiles/test-data-Iris2.txt
    java -jar ./lib/JFML-vx.x.jar Iris Mamdani2 SepalLength 5.1 SepalWidth 3.5 PetalLength 1.4 PetalWidth 0.2
    java -jar ./lib/JFML-vx.x.jar Iris Mamdani3 ./XMLFiles/test-data-Iris1.txt
    java -jar ./lib/JFML-vx.x.jar Iris Mamdani3 PetalWidth 0.5
    java -jar ./lib/JFML-vx.x.jar InvertedPendulum Mamdani1 ./XMLFiles/test-data-InvertedPendulum.txt
    java -jar ./lib/JFML-vx.x.jar InvertedPendulum Mamdani2 ./XMLFiles/test-data-InvertedPendulum.txt
    java -jar ./lib/JFML-vx.x.jar InvertedPendulum TSK1 ./XMLFiles/test-data-InvertedPendulum.txt
    java -jar ./lib/JFML-vx.x.jar InvertedPendulum TSK2 ./XMLFiles/test-data-InvertedPendulum.txt
    java -jar ./lib/JFML-vx.x.jar JapaneseDietAssessment Mamdani ./XMLFiles/test-data-JapaneseDietAssessment.txt
    java -jar ./lib/JFML-vx.x.jar Tipper Mamdani1 ./XMLFiles/test-data-Tipper1.txt
    java -jar ./lib/JFML-vx.x.jar Tipper Mamdani2 ./XMLFiles/test-data-Tipper1.txt
    java -jar ./lib/JFML-vx.x.jar Tipper Mamdani3 ./XMLFiles/test-data-Tipper2.txt
    java -jar ./lib/JFML-vx.x.jar Tipper TSK ./XMLFiles/test-data-Tipper1.txt
    java -jar ./lib/JFML-vx.x.jar Tipper Tsukamoto1 ./XMLFiles/test-data-Tipper1.txt
    java -jar ./lib/JFML-vx.x.jar Tipper Tsukamoto2 ./XMLFiles/test-data-Tipper1.txt
    java -jar ./lib/JFML-vx.x.jar Tipper AnYa ./XMLFiles/test-data-Tipper2.txt
    java -jar ./lib/JFML-vx.x.jar Robot Mamdani ./XMLFiles/test-data-Robot.txt
    java -jar ./lib/JFML-vx.x.jar ./XMLFiles/RobotIEEEstd1855.xml ./XMLFiles/test-data-Robot.txt
    java -jar ./lib/JFML-vx.x.jar ./XMLFiles/RobotIEEEstd1855.xml 2 la av rd 0.2 dq 0.25 o 20 v 0.25
    

Export:

    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/IrisMamdani1.xml ./XMLFiles/IrisMamdani1.fis
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/IrisMamdani1.xml ./XMLFiles/IrisMamdani1.fcl
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/IrisMamdani2.xml ./XMLFiles/IrisMamdani2.fis
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/TipperMamdani1.xml ./XMLFiles/TipperMamdani1.fis
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/TipperMamdani1.xml ./XMLFiles/TipperMamdani1.fcl
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/TipperMamdani2.xml ./XMLFiles/TipperMamdani2.fis
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/TipperMamdani2.xml ./XMLFiles/TipperMamdani2.fcl
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/TipperTSK.xml ./XMLFiles/TipperTSK.fis
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/TipperTSK.xml ./XMLFiles/TipperTSK.fcl
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/IrisMamdani2.xml ./XMLFiles/IrisMamdani2.frbsPMML
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ExportExample ./XMLFiles/TipperTSK.xml ./XMLFiles/TipperTSK.frbsPMML
    

Import:

    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/IrisMamdani1.fis ./XMLFiles/IrisMamdani1.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/IrisMamdani1.fcl ./XMLFiles/IrisMamdani1.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/IrisMamdani2.fis ./XMLFiles/IrisMamdani2.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/TipperMamdani1.fis ./XMLFiles/TipperMamdani1.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/TipperMamdani1.fcl ./XMLFiles/TipperMamdani1.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/TipperMamdani2.fis ./XMLFiles/TipperMamdani2.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/TipperMamdani2.fcl ./XMLFiles/TipperMamdani2.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/TipperTSK.fis ./XMLFiles/TipperTSK.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/TipperTSK.fcl ./XMLFiles/TipperTSK.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/IrisMamdani2.frbsPMML ./XMLFiles/IrisMamdani2.frbsPMML.xml
    java -classpath ./lib/JFML-vx.x.jar jfml.test.ImportExample ./XMLFiles/TipperTSK.frbsPMML ./XMLFiles/TipperTSK.frbsPMML.xml

    

Circular Definitions:

    java -classpath ./lib/JFML-vx.x.jar jfml.test.TaoExample
    

In addition, notice that you can run the examples above by calling to the related bat files in Windows OS or by running the Makefile otherwise.
For example, in Windows OS, running the file main-jfml-CreateIrisMamdaniExampleXML1.bat you can create the file TipperMamdani1.xml. The same example can be executed in Mac or Linux by running the makefile: make createTipperMamdani1. In the same way, you can test the examples by running the bat file main-jfml-test.bat and the corresponding parameters.

Py4JFML

• 1. Download the file py4jfml-x.y.tar.gz in the dist folder (x.y stands for the current version, e.g. 1.0)
• 2. run $ pip3 install py4jfml-x.y.tar.gz

Examples

JFML includes several examples for both users and developers in the package jfml.test. On the one hand, the related Java files are provided in the folder src/jfml/test. On the other hand, the related XML files are provided in the folder XMLFiles. Both folders can be freely downloaded from GitHub.

• Iris (Classification Problem)
• TAO (Classification Problem)
• Inverted Pendulum (Control Problem)
• Tipper (Regression Problem)
• Japanese Diet Assessment (Regression Problem)
• Robot (Real-world Problem)

Let us briefly introduce below these problems as well as the related FLS that we have developed just for illustrative purpose:

Users

Here, we go in detail with 2 of the illustrative examples introduced above:

• Iris (Mamdani1)
• Inverted Pendulum (TSK1)

For each example, we first explain how to create the related XML file and then how to evaluate the FLS.

FuzzyInferenceSystem iris = new FuzzyInferenceSystem("iris - MAMDANI");
KnowledgeBaseType kb = new KnowledgeBaseType();
iris.setKnowledgeBase(kb);

FuzzyVariableType pw = new FuzzyVariableType("PetalWidth", 0.1f, 2.5f);
FuzzyTermType pw_low = new FuzzyTermType("low", FuzzyTermType.TYPE_trapezoidShape, (new float[] { 0.1f, 0.1f, 0.244f, 1.087f }));
pw.addFuzzyTerm(pw_low);
FuzzyTermType pw_medium = new FuzzyTermType("medium", FuzzyTermType.TYPE_trapezoidShape, (new float[] { 0.244f, 1.087f, 1.419f, 1.906f }));
pw.addFuzzyTerm(pw_medium);
FuzzyTermType pw_high = new FuzzyTermType("high", FuzzyTermType.TYPE_trapezoidShape, (new float[] { 1.419f, 1.906f, 2.5f, 2.5f }));
pw.addFuzzyTerm(pw_high);
kb.addVariable(pw);

FuzzyVariableType irisClass = new FuzzyVariableType("irisClass", 1, 3);
irisClass.setDefaultValue(1f);
irisClass.setAccumulation("MAX");
irisClass.setDefuzzifierName("MOM");
irisClass.setType("output");
FuzzyTermType irisClass_setosa = new FuzzyTermType("setosa", FuzzyTermType.TYPE_singletonShape, (new float[] { 1f }));
irisClass.addFuzzyTerm(irisClass_setosa);
FuzzyTermType irisClass_virginica = new FuzzyTermType("virginica", FuzzyTermType.TYPE_singletonShape, (new float[] { 2f }));
irisClass.addFuzzyTerm(irisClass_virginica);
FuzzyTermType irisClass_versicolor = new FuzzyTermType("versicolor", FuzzyTermType.TYPE_singletonShape, (new float[] { 3f }));
irisClass.addFuzzyTerm(irisClass_versicolor);
kb.addVariable(irisClass);

// Create an empty rule base
MamdaniRuleBaseType rb = new MamdaniRuleBaseType("rulebase-iris");

// RULE 1
FuzzyRuleType r1 = new FuzzyRuleType("rule1", "and", "MIN", 1.0f);
AntecedentType ant1 = new AntecedentType();
ant1.addClause(new ClauseType(pw, pw_low));
ConsequentType con1 = new ConsequentType();
con1.addThenClause(irisClass, irisClass_setosa);
r1.setAntecedent(ant1);
r1.setConsequent(con1);
rb.addRule(r1);

// RULE 2
FuzzyRuleType r2 = new FuzzyRuleType("rule2", "and", "MIN", 1.0f);
AntecedentType ant2 = new AntecedentType();
ant2.addClause(new ClauseType(pw, pw_medium));
ConsequentType con2 = new ConsequentType();
con2.addThenClause(irisClass, irisClass_virginica);
r2.setAntecedent(ant2);
r2.setConsequent(con2);
rb.addRule(r2);

// RULE 3
FuzzyRuleType r3 = new FuzzyRuleType("rule3", "and", "MIN", 1.0f);
AntecedentType ant3 = new AntecedentType();
ant3.addClause(new ClauseType(pw, pw_high));
ConsequentType con3 = new ConsequentType();
con3.addThenClause(irisClass, irisClass_versicolor);
r3.setAntecedent(ant3);
r3.setConsequent(con3);
rb.addRule(r3);

// Add rb to the iris FLS
iris.addRuleBase(rb);

File irisXMLFile = new File("./XMLFiles/IrisMamdani1.xml");
JFML.writeFSTtoXML(iris, irisXMLFile);

 
java -jar ./lib/JFML-vx.x.jar Iris Mamdani1 PetalWidth 0.2

1) Loading Fuzzy System from an XML file according the standard IEEE 1855

2) Setting input variables: PetalWidth=0.2

3) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=0.2
 (OUTPUT): irisClass=1.0 

4) Fuzzy System Description

FUZZY SYSTEM: iris - MAMDANI
KNOWLEDGEBASE: 
  *PetalWidth - domain[0.1, 2.5] - input
	low -  trapezoid [a: 0.1, b: 0.1, c: 0.244, d: 1.087]
	medium -  trapezoid [a: 0.244, b: 1.087, c: 1.419, d: 1.906]
	high -  trapezoid [a: 1.419, b: 1.906, c: 2.5, d: 2.5]

  *irisClass - domain[1.0, 3.0] - Accumulation:MAX; Defuzzifier:MOM - output
	setosa -  singleton [a: 1.0]
	virginica -  singleton [a: 2.0]
	versicolor -  singleton [a: 3.0]

RULEBASE:
  *mamdani - rulebase-iris: OR=MAX; AND=MIN; ACTIVATION=MIN
	RULE 1: rule1 - (1.0) IF PetalWidth IS low THEN irisClass IS setosa [weight=1.0]
	RULE 2: rule2 - (0.0) IF PetalWidth IS medium THEN irisClass IS virginica [weight=1.0]
	RULE 3: rule3 - (0.0) IF PetalWidth IS high THEN irisClass IS versicolor [weight=1.0]

java -jar ./lib/JFML-vx.x.jar Iris Mamdani1 ./XMLFiles/test-data-Iris1.txt

1) Loading Fuzzy System from an XML file according the standard IEEE 1855

2.0) Setting input variables: PetalWidth=0.2

3.0) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=0.2
 (OUTPUT): irisClass=1.0 

2.1) Setting input variables: PetalWidth=0.35

3.1) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=0.35
 (OUTPUT): irisClass=1.0 

2.2) Setting input variables: PetalWidth=0.55

3.2) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=0.55
 (OUTPUT): irisClass=1.0 

2.3) Setting input variables: PetalWidth=0.65

3.3) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=0.65
 (OUTPUT): irisClass=1.0 

2.4) Setting input variables: PetalWidth=0.82

3.4) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=0.82
 (OUTPUT): irisClass=2.0 

2.5) Setting input variables: PetalWidth=1.25

3.5) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=1.25
 (OUTPUT): irisClass=2.0 

2.6) Setting input variables: PetalWidth=1.54

3.6) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=1.54
 (OUTPUT): irisClass=2.0 

2.7) Setting input variables: PetalWidth=1.66

3.7) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=1.66
 (OUTPUT): irisClass=2.0 

2.8) Setting input variables: PetalWidth=1.75

3.8) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=1.75
 (OUTPUT): irisClass=3.0 

2.9) Setting input variables: PetalWidth=2.0

3.9) Making fuzzy inference
RESULTS
 (INPUT): PetalWidth=2.0
 (OUTPUT): irisClass=3.0 

4) Fuzzy System Description

FUZZY SYSTEM: iris - MAMDANI
KNOWLEDGEBASE: 
  *PetalWidth - domain[0.1, 2.5] - input
	low -  trapezoid [a: 0.1, b: 0.1, c: 0.244, d: 1.087]
	medium -  trapezoid [a: 0.244, b: 1.087, c: 1.419, d: 1.906]
	high -  trapezoid [a: 1.419, b: 1.906, c: 2.5, d: 2.5]

  *irisClass - domain[1.0, 3.0] - Accumulation:MAX; Defuzzifier:MOM - output
	setosa -  singleton [a: 1.0]
	virginica -  singleton [a: 2.0]
	versicolor -  singleton [a: 3.0]

RULEBASE:
  *mamdani - rulebase-iris: OR=MAX; AND=MIN; ACTIVATION=MIN
	RULE 1: rule1 - (0.0) IF PetalWidth IS low THEN irisClass IS setosa [weight=1.0]
	RULE 2: rule2 - (0.0) IF PetalWidth IS medium THEN irisClass IS virginica [weight=1.0]
	RULE 3: rule3 - (1.0) IF PetalWidth IS high THEN irisClass IS versicolor [weight=1.0]

FuzzyInferenceSystem invertedPendulum = new FuzzyInferenceSystem("invertedPendulum - TSK");
KnowledgeBaseType kb = new KnowledgeBaseType();
invertedPendulum.setKnowledgeBase(kb);

//FUZZY VARIABLE Angle
FuzzyVariableType ang = new FuzzyVariableType("Angle", 0, 255);

// Basic linguistic terms
FuzzyTermType ang_vneg = new FuzzyTermType("very negative", FuzzyTermType.TYPE_trapezoidShape, (new float[] { 0f, 0f, 48f, 88f }));
ang.addFuzzyTerm(ang_vneg);
FuzzyTermType ang_neg = new FuzzyTermType("negative", FuzzyTermType.TYPE_triangularShape, (new float[] { 48f, 88f, 128f }));
ang.addFuzzyTerm(ang_neg);
FuzzyTermType ang_neu = new FuzzyTermType("zero", FuzzyTermType.TYPE_triangularShape, (new float[] { 88f, 128f, 168f }));
ang.addFuzzyTerm(ang_neu);
FuzzyTermType ang_pos = new FuzzyTermType("positive", FuzzyTermType.TYPE_triangularShape, (new float[] { 128f, 168f, 208f }));
ang.addFuzzyTerm(ang_pos);
FuzzyTermType ang_vpos = new FuzzyTermType("very positive", FuzzyTermType.TYPE_trapezoidShape, (new float[] { 168f, 208f, 255f, 255f }));
ang.addFuzzyTerm(ang_vpos);

// OR composite linguistic terms
OrLogicalType ang_or1 = new OrLogicalType("BSUM", "very negative", "negative");
CircularDefinitionType ang_c1 = new CircularDefinitionType(ang_or1, ang);
FuzzyTermType ang_vneg_or_neg = new FuzzyTermType("very negative or negative", ang_c1);
ang.addFuzzyTerm(ang_vneg_or_neg);
OrLogicalType ang_or2 = new OrLogicalType("BSUM", "positive", "very positive");
CircularDefinitionType ang_c2 = new CircularDefinitionType(ang_or2, ang);
FuzzyTermType ang_pos_or_vpos = new FuzzyTermType("positive or very positive", ang_c2);
ang.addFuzzyTerm(ang_pos_or_vpos);
kb.addVariable(ang);

//FUZZY VARIABLE ChangeAngle
FuzzyVariableType ca = new FuzzyVariableType("ChangeAngle", 0, 255);

// Basic linguistic terms
FuzzyTermType ca_vneg = new FuzzyTermType("very negative", FuzzyTermType.TYPE_trapezoidShape, (new float[] { 0f, 0f, 48f, 88f }));
ca.addFuzzyTerm(ca_vneg);
FuzzyTermType ca_neg = new FuzzyTermType("negative", FuzzyTermType.TYPE_triangularShape, (new float[] { 48f, 88f, 128f }));
ca.addFuzzyTerm(ca_neg);
FuzzyTermType ca_neu = new FuzzyTermType("zero", FuzzyTermType.TYPE_triangularShape, (new float[] { 88f, 128f, 168f }));
ca.addFuzzyTerm(ca_neu);
FuzzyTermType ca_pos = new FuzzyTermType("positive", FuzzyTermType.TYPE_triangularShape, (new float[] { 128f, 168f, 208f }));
ca.addFuzzyTerm(ca_pos);
FuzzyTermType ca_vpos = new FuzzyTermType("very positive", FuzzyTermType.TYPE_trapezoidShape, (new float[] { 168f, 208f, 255f, 255f }));
ca.addFuzzyTerm(ca_vpos);

// OR composite linguistic terms
OrLogicalType ca_or1 = new OrLogicalType("BSUM", "very negative", "negative");
CircularDefinitionType ca_c1 = new CircularDefinitionType(ca_or1, ca);
FuzzyTermType ca_vneg_or_neg = new FuzzyTermType("very negative or negative", ca_c1);
ca.addFuzzyTerm(ca_vneg_or_neg);
OrLogicalType ca_or2 = new OrLogicalType("BSUM", "positive", "very positive");
CircularDefinitionType ca_c2 = new CircularDefinitionType(ca_or2, ang);
FuzzyTermType ca_pos_or_vpos = new FuzzyTermType("positive or very positive", ca_c2);
ca.addFuzzyTerm(ca_pos_or_vpos);
kb.addVariable(ca);

TskVariableType force = new TskVariableType("Force");
force.setDefaultValue(0f);
force.setCombination("WA");
force.setType("output");
TskTermType force_vneg = new TskTermType("very negative", TskTerm._ORDER_0, (new float[] { 48f}));
force.addTskTerm(force_vneg);
TskTermType force_neg = new TskTermType("negative", TskTerm._ORDER_0, (new float[] { 88f}));
force.addTskTerm(force_neg);
TskTermType force_neu = new TskTermType("zero", TskTerm._ORDER_0, (new float[] { 128f}));
force.addTskTerm(force_neu);
TskTermType force_pos = new TskTermType("positive", TskTerm._ORDER_0, (new float[] { 168f}));
force.addTskTerm(force_pos);
TskTermType force_vpos = new TskTermType("very positive", TskTerm._ORDER_0, (new float[] { 208f}));
force.addTskTerm(force_vpos);
kb.addVariable(force);

// Create an empty rule base
TskRuleBaseType rb = new TskRuleBaseType("rulebase1", FuzzySystemRuleBase.TYPE_TSK);
// RULE 1
TskFuzzyRuleType r1 = new TskFuzzyRuleType("rule1", "and", "MIN", 1.0f);
AntecedentType ant1 = new AntecedentType();
ant1.addClause(new ClauseType(ang, ang_vneg_or_neg));
ant1.addClause(new ClauseType(ca, ca_vneg_or_neg));
TskConsequentType con1 = new TskConsequentType();
con1.addTskThenClause(force, force_vneg);
r1.setAntecedent(ant1);
r1.setTskConsequent(con1);
rb.addTskRule(r1);
// RULE 2
TskFuzzyRuleType r2 = new TskFuzzyRuleType("rule2", "and", "MIN", 1.0f);
AntecedentType ant2 = new AntecedentType();
ant2.addClause(new ClauseType(ang, ang_vneg));
ant2.addClause(new ClauseType(ca, ca_neu));
TskConsequentType con2 = new TskConsequentType();
con2.addTskThenClause(force, force_vneg);
r2.setAntecedent(ant2);
r2.setTskConsequent(con2);
rb.addTskRule(r2);
// RULE 3
TskFuzzyRuleType r3 = new TskFuzzyRuleType("rule3", "and", "MIN", 1.0f);
AntecedentType ant3 = new AntecedentType();
ant3.addClause(new ClauseType(ang, ang_vneg));
ant3.addClause(new ClauseType(ca, ca_pos));
TskConsequentType con3 = new TskConsequentType();
con3.addTskThenClause(force, force_neg);
r3.setAntecedent(ant3);
r3.setTskConsequent(con3);
rb.addTskRule(r3);
// RULE 4
TskFuzzyRuleType r4 = new TskFuzzyRuleType("rule4", "and", "MIN", 1.0f);
AntecedentType ant4 = new AntecedentType();
ant4.addClause(new ClauseType(ang, ang_vneg));
ant4.addClause(new ClauseType(ca, ca_vpos));
TskConsequentType con4 = new TskConsequentType();
con4.addTskThenClause(force, force_neu);
r4.setAntecedent(ant4);
r4.setTskConsequent(con4);
rb.addTskRule(r4);
// RULE 5
TskFuzzyRuleType r5 = new TskFuzzyRuleType("rule5", "and", "MIN", 1.0f);
AntecedentType ant5 = new AntecedentType();
ant5.addClause(new ClauseType(ang, ang_neg));
ant5.addClause(new ClauseType(ca, ca_neu));
TskConsequentType con5 = new TskConsequentType();
con5.addTskThenClause(force, force_neg);
r5.setAntecedent(ant5);
r5.setTskConsequent(con5);
rb.addTskRule(r5);
// RULE 6
TskFuzzyRuleType r6 = new TskFuzzyRuleType("rule6", "and", "MIN", 1.0f);
AntecedentType ant6 = new AntecedentType();
ant6.addClause(new ClauseType(ang, ang_neg));
ant6.addClause(new ClauseType(ca, ca_pos));
TskConsequentType con6 = new TskConsequentType();
con6.addTskThenClause(force, force_neu);
r6.setAntecedent(ant6);
r6.setTskConsequent(con6);
rb.addTskRule(r6);
// RULE 7
TskFuzzyRuleType r7 = new TskFuzzyRuleType("rule7", "and", "MIN", 1.0f);
AntecedentType ant7 = new AntecedentType();
ant7.addClause(new ClauseType(ang, ang_neg));
ant7.addClause(new ClauseType(ca, ca_vpos));
TskConsequentType con7 = new TskConsequentType();
con7.addTskThenClause(force, force_pos);
r7.setAntecedent(ant7);
r7.setTskConsequent(con7);
rb.addTskRule(r7);
// RULE 8
TskFuzzyRuleType r8 = new TskFuzzyRuleType("rule8", "and", "MIN", 1.0f);
AntecedentType ant8 = new AntecedentType();
ant8.addClause(new ClauseType(ang, ang_neu));
ant8.addClause(new ClauseType(ca, ca_vneg));
TskConsequentType con8 = new TskConsequentType();
con8.addTskThenClause(force, force_vneg);
r8.setAntecedent(ant8);
r8.setTskConsequent(con8);
rb.addTskRule(r8);
// RULE 9
TskFuzzyRuleType r9 = new TskFuzzyRuleType("rule9", "and", "MIN", 1.0f);
AntecedentType ant9 = new AntecedentType();
ant9.addClause(new ClauseType(ang, ang_neu));
ant9.addClause(new ClauseType(ca, ca_neg));
TskConsequentType con9 = new TskConsequentType();
con9.addTskThenClause(force, force_neg);
r9.setAntecedent(ant9);
r9.setTskConsequent(con9);
rb.addTskRule(r9);
// RULE 10
TskFuzzyRuleType r10 = new TskFuzzyRuleType("rule10", "and", "MIN", 1.0f);
AntecedentType ant10 = new AntecedentType();
ant10.addClause(new ClauseType(ang, ang_neu));
ant10.addClause(new ClauseType(ca, ca_neu));
TskConsequentType con10 = new TskConsequentType();
con10.addTskThenClause(force, force_neu);
r10.setAntecedent(ant10);
r10.setTskConsequent(con10);
rb.addTskRule(r10);
// RULE 11
TskFuzzyRuleType r11 = new TskFuzzyRuleType("rule11", "and", "MIN", 1.0f);
AntecedentType ant11 = new AntecedentType();
ant11.addClause(new ClauseType(ang, ang_neu));
ant11.addClause(new ClauseType(ca, ca_pos));
TskConsequentType con11 = new TskConsequentType();
con11.addTskThenClause(force, force_pos);
r11.setAntecedent(ant11);
r11.setTskConsequent(con11);
rb.addTskRule(r11);
// RULE 12
TskFuzzyRuleType r12 = new TskFuzzyRuleType("rule12", "and", "MIN", 1.0f);
AntecedentType ant12 = new AntecedentType();
ant12.addClause(new ClauseType(ang, ang_neu));
ant12.addClause(new ClauseType(ca, ca_vpos));
TskConsequentType con12 = new TskConsequentType();
con12.addTskThenClause(force, force_vpos);
r12.setAntecedent(ant12);
r12.setTskConsequent(con12);
rb.addTskRule(r12);
// RULE 13
TskFuzzyRuleType r13 = new TskFuzzyRuleType("rule13", "and", "MIN", 1.0f);
AntecedentType ant13 = new AntecedentType();
ant13.addClause(new ClauseType(ang, ang_pos));
ant13.addClause(new ClauseType(ca, ca_vneg));
TskConsequentType con13 = new TskConsequentType();
con13.addTskThenClause(force, force_neg);
r13.setAntecedent(ant13);
r13.setTskConsequent(con13);
rb.addTskRule(r13);
// RULE 14
TskFuzzyRuleType r14 = new TskFuzzyRuleType("rule14", "and", "MIN", 1.0f);
AntecedentType ant14 = new AntecedentType();
ant14.addClause(new ClauseType(ang, ang_pos));
ant14.addClause(new ClauseType(ca, ca_neg));
TskConsequentType con14 = new TskConsequentType();
con14.addTskThenClause(force, force_neu);
r14.setAntecedent(ant14);
r14.setTskConsequent(con14);
rb.addTskRule(r14);
// RULE 15
TskFuzzyRuleType r15 = new TskFuzzyRuleType("rule15", "and", "MIN", 1.0f);
AntecedentType ant15 = new AntecedentType();
ant15.addClause(new ClauseType(ang, ang_pos));
ant15.addClause(new ClauseType(ca, ca_neu));
TskConsequentType con15 = new TskConsequentType();
con15.addTskThenClause(force, force_pos);
r15.setAntecedent(ant15);
r15.setTskConsequent(con15);
rb.addTskRule(r15);
// RULE 16
TskFuzzyRuleType r16 = new TskFuzzyRuleType("rule16", "and", "MIN", 1.0f);
AntecedentType ant16 = new AntecedentType();
ant16.addClause(new ClauseType(ang, ang_vpos));
ant16.addClause(new ClauseType(ca, ca_vneg));
TskConsequentType con16 = new TskConsequentType();
con16.addTskThenClause(force, force_neu);
r16.setAntecedent(ant16);
r16.setTskConsequent(con16);
rb.addTskRule(r16);
// RULE 17
TskFuzzyRuleType r17 = new TskFuzzyRuleType("rule17", "and", "MIN", 1.0f);
AntecedentType ant17 = new AntecedentType();
ant17.addClause(new ClauseType(ang, ang_vpos));
ant17.addClause(new ClauseType(ca, ca_neg));
TskConsequentType con17 = new TskConsequentType();
con17.addTskThenClause(force, force_pos);
r17.setAntecedent(ant17);
r17.setTskConsequent(con17);
rb.addTskRule(r17);
// RULE 18
TskFuzzyRuleType r18 = new TskFuzzyRuleType("rule18", "and", "MIN", 1.0f);
AntecedentType ant18 = new AntecedentType();
ant18.addClause(new ClauseType(ang, ang_vpos));
ant18.addClause(new ClauseType(ca, ca_neu));
TskConsequentType con18 = new TskConsequentType();
con18.addTskThenClause(force, force_vpos);
r18.setAntecedent(ant18);
r18.setTskConsequent(con18);
rb.addTskRule(r18);
// RULE 19
TskFuzzyRuleType r19 = new TskFuzzyRuleType("rule19", "and", "MIN", 1.0f);
AntecedentType ant19 = new AntecedentType();
ant19.addClause(new ClauseType(ang, ang_pos_or_vpos));
ant19.addClause(new ClauseType(ca, ca_pos_or_vpos));
TskConsequentType con19 = new TskConsequentType();
con19.addTskThenClause(force, force_vpos);
r19.setAntecedent(ant19);
r19.setTskConsequent(con19);
rb.addTskRule(r19);
// Add rb to the invertedPendulum FLS
invertedPendulum.addRuleBase(rb);

File invertedPendulumXMLFile = new File("./XMLFiles/InvertedPendulumTSK1.xml");
JFML.writeFSTtoXML(invertedPendulum, invertedPendulumXMLFile);

java -jar ./lib/JFML-vx.x.jar InvertedPendulum TSK1 ./XMLFiles/test-data-InvertedPendulum.txt

1) Loading Fuzzy System from an XML file according the standard IEEE 1855

2.0) Setting input variables: Angle=10.0, ChangeAngle=10.0

3.0) Making fuzzy inference
RESULTS
 (INPUT): Angle=10.0, ChangeAngle=10.0
 (OUTPUT): Force=48.0 

2.1) Setting input variables: Angle=125.0, ChangeAngle=125.0

3.1) Making fuzzy inference
RESULTS
 (INPUT): Angle=125.0, ChangeAngle=125.0
 (OUTPUT): Force=117.565216 

2.2) Setting input variables: Angle=250.0, ChangeAngle=250.0

3.2) Making fuzzy inference
RESULTS
 (INPUT): Angle=250.0, ChangeAngle=250.0
 (OUTPUT): Force=208.0 

4) Fuzzy System Description

FUZZY SYSTEM: invertedPendulum - TSK
KNOWLEDGEBASE: 
  *Angle - domain[0.0, 255.0] - input
	very negative -  trapezoid [a: 0.0, b: 0.0, c: 48.0, d: 88.0]
	negative -  triangular [a: 48.0, b: 88.0, c: 128.0]
	zero -  triangular [a: 88.0, b: 128.0, c: 168.0]
	positive -  triangular [a: 128.0, b: 168.0, c: 208.0]
	very positive -  trapezoid [a: 168.0, b: 208.0, c: 255.0, d: 255.0]
	very negative or negative -  very negative OR negative
	positive or very positive -  positive OR very positive

  *ChangeAngle - domain[0.0, 255.0] - input
	very negative -  trapezoid [a: 0.0, b: 0.0, c: 48.0, d: 88.0]
	negative -  triangular [a: 48.0, b: 88.0, c: 128.0]
	zero -  triangular [a: 88.0, b: 128.0, c: 168.0]
	positive -  triangular [a: 128.0, b: 168.0, c: 208.0]
	very positive -  trapezoid [a: 168.0, b: 208.0, c: 255.0, d: 255.0]
	very negative or negative -  very negative OR negative
	positive or very positive -  positive OR very positive

  *Force - output
	very negative - z = 48.0
	negative - z = 88.0
	zero - z = 128.0
	positive - z = 168.0
	very positive - z = 208.0

RULEBASE:
  *tsk - rulebase1: OR=MAX; AND=MIN; ACTIVATION=MIN
	RULE 1: rule1 - (0.0) IF Angle IS very negative or negative AND ChangeAngle IS very negative or negative THEN Force IS very negative [weight=1.0]
	RULE 2: rule2 - (0.0) IF Angle IS very negative AND ChangeAngle IS zero THEN Force IS very negative [weight=1.0]
	RULE 3: rule3 - (0.0) IF Angle IS very negative AND ChangeAngle IS positive THEN Force IS negative [weight=1.0]
	RULE 4: rule4 - (0.0) IF Angle IS very negative AND ChangeAngle IS very positive THEN Force IS zero [weight=1.0]
	RULE 5: rule5 - (0.0) IF Angle IS negative AND ChangeAngle IS zero THEN Force IS negative [weight=1.0]
	RULE 6: rule6 - (0.0) IF Angle IS negative AND ChangeAngle IS positive THEN Force IS zero [weight=1.0]
	RULE 7: rule7 - (0.0) IF Angle IS negative AND ChangeAngle IS very positive THEN Force IS positive [weight=1.0]
	RULE 8: rule8 - (0.0) IF Angle IS zero AND ChangeAngle IS very negative THEN Force IS very negative [weight=1.0]
	RULE 9: rule9 - (0.0) IF Angle IS zero AND ChangeAngle IS negative THEN Force IS negative [weight=1.0]
	RULE 10: rule10 - (0.0) IF Angle IS zero AND ChangeAngle IS zero THEN Force IS zero [weight=1.0]
	RULE 11: rule11 - (0.0) IF Angle IS zero AND ChangeAngle IS positive THEN Force IS positive [weight=1.0]
	RULE 12: rule12 - (0.0) IF Angle IS zero AND ChangeAngle IS very positive THEN Force IS very positive [weight=1.0]
	RULE 13: rule13 - (0.0) IF Angle IS positive AND ChangeAngle IS very negative THEN Force IS negative [weight=1.0]
	RULE 14: rule14 - (0.0) IF Angle IS positive AND ChangeAngle IS negative THEN Force IS zero [weight=1.0]
	RULE 15: rule15 - (0.0) IF Angle IS positive AND ChangeAngle IS zero THEN Force IS positive [weight=1.0]
	RULE 16: rule16 - (0.0) IF Angle IS very positive AND ChangeAngle IS very negative THEN Force IS zero [weight=1.0]
	RULE 17: rule17 - (0.0) IF Angle IS very positive AND ChangeAngle IS negative THEN Force IS positive [weight=1.0]
	RULE 18: rule18 - (0.0) IF Angle IS very positive AND ChangeAngle IS zero THEN Force IS very positive [weight=1.0]
	RULE 19: rule19 - (1.0) IF Angle IS positive or very positive AND ChangeAngle IS positive or very positive THEN Force IS very positive [weight=1.0]

Developers

Here, we provide developers with some details about programming code for 2 of the illustrative examples introduced above:

• Japanese Diet Assessment
• Tipper (Mamdani3)

File xml = new File("./XMLFiles/JapaneseDietAssessmentMamdani.xml");
//loading FLS from an XML file according to the standard IEEE 1855
FuzzyInferenceSystem fs = JFML.load(xml);

KnowledgeBaseVariable input1 =  fs.getVariable("PCC");
KnowledgeBaseVariable input2 =  fs.getVariable("PCP");
KnowledgeBaseVariable input3 =  fs.getVariable("PCF");
KnowledgeBaseVariable input4 =  fs.getVariable("PCR");
KnowledgeBaseVariable input5 =  fs.getVariable("FGB");
input1.setValue(45.0);
input2.setValue(21.6);
input3.setValue(31.1);
input4.setValue(82.9);
input5.setValue(3.95);

fs.evaluate();	

// get inferred output
KnowledgeBaseVariable output =  fs.getVariable("DHL");
float value = output.getValue();

//Printing results
System.out.println("RESULTS");
System.out.println(" (INPUT1): "+input1.getName()+ "="+input1.getValue());
System.out.println(" (INPUT2): "+input2.getName()+ "="+input2.getValue());
System.out.println(" (INPUT3): "+input3.getName()+ "="+input3.getValue());
System.out.println(" (INPUT4): "+input4.getName()+ "="+input4.getValue());
System.out.println(" (INPUT5): "+input5.getName()+ "="+input5.getValue());
System.out.println(" (OUTPUT): "+output.getName()+"="+ value);
//Printing textual description of the FuzzySystem
System.out.println(fs.toString());

AggregatedFuzzyVariableType quality = new AggregatedFuzzyVariableType("quality");

// AGGREGATED FUZZY TERM acceptable
AggregatedFuzzyTermType acceptable = new AggregatedFuzzyTermType("acceptable");
ClauseType acceptable_t1 = new ClauseType(food,delicious);
ClauseType acceptable_t2 = new ClauseType(service,good);
ClauseType acceptable_t3 = new ClauseType(service,excellent);
OrAggregatedType acceptable_or = new OrAggregatedType(acceptable_t2, acceptable_t3);
AndAggregatedType acceptable_and = new AndAggregatedType(acceptable_t1, acceptable_or);
acceptable.setAnd(acceptable_and);

// AGGREGATED FUZZY TERM bad
AggregatedFuzzyTermType bad = new AggregatedFuzzyTermType("bad");
ClauseType bad_t1 = new ClauseType(food,rancid);
ClauseType bad_t2 = new ClauseType(service,poor);
OrAggregatedType bad_or = new OrAggregatedType(bad_t1, bad_t2);
bad.setOr(bad_or);
quality.addAggregatedFuzzyTerm(acceptable);
quality.addAggregatedFuzzyTerm(bad);
kb.addVariable(quality);

private float custom_and(float x, float y, String act) {
	// TODO 
	return 0;
}
private float custom_or(float x, float y, String orMethod) {
	// TODO
	return 0;
}

// RULE 4
FuzzyRuleType rule4 = new FuzzyRuleType("rule4", "or", "MAX", 1.0f);
AntecedentType ant4 = new AntecedentType();
ant4.addClause(new ClauseType(quality, acceptable));
ConsequentType con4 = new ConsequentType();
con4.addThenClause(tip, generous);
rule4.setAntecedent(ant4);
rule4.setConsequent(con4);
rb.addRule(rule4);

// RULE 5
FuzzyRuleType rule5 = new FuzzyRuleType("rule5", "or", "MAX", 1.0f);
AntecedentType ant5 = new AntecedentType();
ant5.addClause(new ClauseType(quality, bad, "very"));
ConsequentType con5 = new ConsequentType();
con5.addThenClause(tip, cheap);
rule5.setAntecedent(ant5);
rule5.setConsequent(con5);
rb.addRule(rule5);

Embedded System examples

• Home-made mobile robot for wall-following
• Ventilation system for a refrigerating chamber

Home-made mobile robot for wall-following

We have developed a home-made mobile robot with low-cost components for this example. The architecture of this robot consists of an Arduino MEGA 2560 connected via USB with a Raspberry Pi, five ultrasonic sensors HC-SR04, one accelerometer/gyroscope sensor MPU6050, a servo SG-90 and two DC drive motors with matching wheels and driver H-Bridge L298N.

Hardware architecture and a photography of our home-made mobile robot:

In this case, a Raspberry Pi is used as a remote computer where the fuzzy inference is performed by taking the input values (from ultrasonic and accelerometer/gyroscope sensors) which are connected to the Arduino board. In other words, the FLC is embedded in the Arduino board but the fuzzy inference is carried out in the Raspberry Pi (where JFML is installed).

Notice that the sensor values are not directly used as inputs of the FLC (RobotIEEEstd1855.xml). They are low-level input variables that do not provide by themselves information that is relevant and meaningful to the FLC. For this reason, these low-level values are aggregated in JFML by means of the AggregatedSensor class in order to generate high-level input variables for the FLC. Likewise, the FLC outputs are sent to other aggregated sensors to calculate the values that will be sent to the DC motors and the servo for the linear acceleration and the angular velocity respectively.

The necessary steps to run the FLC with the Embedded System module are as follows. The first step is to read the description of the FLC from the related FML/XML document.

File fml=new File("./Examples/XMLFiles/RobotIEEEstd1855.xml");
FuzzyInferenceSystem fs = JFML.load(fml);

The second step is to instantiate the sensors/actuators that are connected with the Arduino board.

KnowledgeBaseVariable rd =  fs.getVariable("rd");
KnowledgeBaseVariable dq =  fs.getVariable("dq");
KnowledgeBaseVariable o =  fs.getVariable("o");
KnowledgeBaseVariable v =  fs.getVariable("v");
KnowledgeBaseVariable la =  fs.getVariable("la");
KnowledgeBaseVariable av =  fs.getVariable("av");

Sensor rdSF = new ArduinoHC_SR04(rd.getName()+"front", ArduinoPin.PIN_40, ArduinoPin.PIN_41, 10, 200, true, 3, true, true);
Sensor rdSF2 = new ArduinoHC_SR04(rd.getName()+"front2", ArduinoPin.PIN_48, ArduinoPin.PIN_49, true, 3, false,true);
Sensor rdSR = new ArduinoHC_SR04(rd.getName()+"right", ArduinoPin.PIN_50, ArduinoPin.PIN_51, true, 3, false,true);
Sensor rdSR2 = new ArduinoHC_SR04(rd.getName()+"right2", ArduinoPin.PIN_32, ArduinoPin.PIN_33, true, 3,false, true);
Sensor dqSL = new ArduinoHC_SR04(dq.getName()+"left", ArduinoPin.PIN_30, ArduinoPin.PIN_31, true, 3, false,true);
Sensor oS = new ArduinoMPU6050(o.getName(), -45, 45, true);
Sensor laS = new ArduinoH_BRIDGE_L298N(la.getName(), ArduinoPin.PIN_6, ArduinoPin.PIN_7, ArduinoPin.PIN_4, ArduinoPin.PIN_2, ArduinoPin.PIN_1, ArduinoPin.PIN_5, -1, 1, 40, 70, 15);
Sensor avS = new ArduinoSERVO(av.getName(), ArduinoPin.PIN_9, -1, 1, 45, 135, 45, true);

The third step is to generate the aggregated sensors for the input and output values.

ArrayList sensorsRD = new ArrayList<>();
sensorsRD.add(rdSF);
sensorsRD.add(rdSF2);
sensorsRD.add(rdSR);
sensorsRD.add(rdSR2);

AggregatedSensor rdAgg, dqAgg, oAgg, avAgg, vAgg;
ArrayList sensorsDQ, sensorsO, sensorsAV;

rdAgg = new ArduinoAggregatedSensorRD(rd.getName(), sensorsRD, 0, 3, 6, 50, true);
sensorsDQ = new ArrayList<>();
sensorsDQ.add(dqSL);
dqAgg = new ArduinoAggregatedSensorDQ( dq.getName(), sensorsDQ, 0, 2);

sensorsO = new ArrayList<>();
sensorsO.add(rdSR);
sensorsO.add(rdSR2);
oAgg = new ArduinoAggregatedSensorO(o.getName(), sensorsO, -45, 45);
sensorsAV = new ArrayList<>();
sensorsAV.add(avS);
vAgg = new ArduinoAggregatedSensorV(v.getName(), -1, 1, 50);
avAgg = new ArduinoAggregatedSensorAV(av.getName(), sensorsAV, -1, 1, 18);

The fourth step is to map the input/output variables with the sensors/actuators and to include them in a list.

ArrayList eVar = new ArrayList<>();
eVar.add(new EmbeddedVariableArduino(0,rd,rdSF));
eVar.add(new EmbeddedVariableArduino(0,rd,rdSF2));
eVar.add(new EmbeddedVariableArduino(0,rd,rdSR));
eVar.add(new EmbeddedVariableArduino(0,rd,rdSR2));
eVar.add(new EmbeddedVariableArduino(0,rd,rdAgg));
eVar.add(new EmbeddedVariableArduino(1,dq,dqSL));
eVar.add(new EmbeddedVariableArduino(1,dq,dqAgg));
eVar.add(new EmbeddedVariableArduino(2,o,oS));
eVar.add(new EmbeddedVariableArduino(2,o,oAgg));
eVar.add(new EmbeddedVariableArduino(3,v,vAgg));
eVar.add(new EmbeddedVariableArduino(4,la,laS));
eVar.add(new EmbeddedVariableArduino(5,av,avS));
eVar.add(new EmbeddedVariableArduino(5,av,avAgg));

The fifth step is to create the embedded system (including the name, port, rate, etc.)

EmbeddedSystem robot = new EmbeddedSystemArduinoUSB("Robot","USB_PORT", 9600, eVar);

An .ino file can be automatically created and ready to be written in the Arduino board with the IDE provided by the company, and then the board can be connected to the Raspberry through a USB connection.

robot.createRunnableEmbeddedFile("RobotIEEEstd1855_Arduino.ino");

Finally, the embedded system is associated to the FLC and we can run the system with the next Java code:

ArrayList embd_R = new ArrayList<>();
embd_R(robot);

EmbeddedController controller = new EmbeddedControllerSystem(embd_R,fs);
controller.run();

Related files:

• Robot_Arduino.java
• RobotIEEEstd1855_Arduino.ino
• RobotIEEEstd1855.xml

Ventilation system for a refrigerating chamber

In this example a FLC has been designed to manage a ventilation system for a refrigerating chamber in order to show the use of the three communication mechanisms (WiFi, Bluetooth and USB) and the two embedded systems (Arduino and Raspberry Pi) available in the JFML. This kind of fuzzy controller is commonly considered in the food-processing industry due to the fact that the chilled and frozen food should be conserved in specific conditions to maintain their nutritional properties. Fuzzy controllers can preserve the original cooling conditions while avoiding abrupt changes in the environment.

It is made up of three modules (an Arduino UNO board, a NodeMCU, and a Raspberry Pi), two temperature and humidity sensors DHT22, a proximity sensor HCSR04, and a DC motor. The sensors DHT22 are connected to the NodeMCU and the Arduino UNO to measure the temperature and the humidity, respectively. The sensor HCSR04 is connected to the Raspberry Pi for measuring the proximity. In addition, the DC motor is connected to the Arduino UNO to control the FAN power of the chamber. Moreover, a remote personal computer (where JFML is installed) is used to manage the whole system in real-time. The JFML library let us running the related FLC and to infer the output values from the input values. The computer is connected to the NodeMCU via WiFi, to the Arduino Uno via USB and to the Raspberry Pi via Bluetooth.

The hardware architecture for the ventilation system:

The necessary steps to run the FLC with the Embedded System module are as follows:
The first step is to read the description of the FLC from the related FML/XML document.

File fml=new File("./Examples/XMLFiles/Chamber.xml");
FuzzyInferenceSystem fs = JFML.load(fml);

The second step is to create the sensors/actuators that are connected with the Arduino board.

KnowledgeBaseVariable temp, hum, prox, power;
temp = fs.getVariable("temperature");
hum = fs.getVariable("humidity");
prox = fs.getVariable("proximity");
power = fs.getVariable("power");

Sensor tempS, humS, proxS, powerS;	
tempS = new ArduinoDHT22_temperature(temp.getName(), ArduinoPin.PIN_D2);
humS = new ArduinoDHT22_humidity(hum.getName(), ArduinoPin.PIN_2);
powerS = new ArduinoDCMOTOR_PWM(power.getName(), ArduinoPin.PIN_10, ArduinoPin.PIN_11);
proxS = new RaspberryHC_SR04(prox.getName(), RaspberryPin.GPIO25, RaspberryPin.GPIO7);

The third step is to map the input/output variables with the sensors/actuators and to include them in a list.

ArrayList eVarWIFI;
eVarWIFI = new ArrayList<>();
eVarWIFI.add(new EmbeddedVariableArduino(0, temp, tempS));

ArrayList eVarUSB;
eVarUSB = new ArrayList<>();
eVarUSB.add(new EmbeddedVariableArduino(0, hum, humS));
eVarUSB.add(new EmbeddedVariableArduino(1, power, powerS));

ArrayList eVarBluetooth;
eVarBluetooth = new ArrayList<>();
eVarBluetooth.add(new EmbeddedVariableRaspberry(0, prox, proxS));

The fourth step is to create the embedded system (including the name, port, rate, etc.)

EmbeddedSystem arduinoWIFI = new EmbeddedSystemArduinoWifi("arduinoWIFIDHT22TEMP", "IP_ADDRESS", "SSID", "PASSWORD", eVarWIFI);
EmbeddedSystem arduinoUSB = new EmbeddedSystemArduinoUsb("arduinoUSB-DHT22HUM", "USB_PORT", 9600, eVarUSB);
EmbeddedSystem rpiBluetooth = new embeddedSystemRaspberryBluetooth("rpiBluetooth-HCSR04","BLUETOOTH_PORT", 9600, eVarBluetooth);

Runnable files can be automatically generated. The .ino file is ready to be written in the Arduino board with the IDE provided by the company and the .py file has to be executed by the command "python file.py" in the Raspberry Pi. The following code lines are used to genereta the runnable files:

arduinoWIFI.createRunnableEmbeddedFile(fml.getName()+"WIFI");
arduinoUSB.createRunnableEmbeddedFile(fml.getName()+"USB");
rpyBluetooth.createRunnableEmbeddedFile(fml.getName()+"BLUETOOTH");

Finally, we can execute the controller that synchronizes all the embedded systems (Arduino UNO, NodeMCU and Raspberry Pi) and runs the FLC, in this case in the external computer. The following Java code corresponds to this final step:

ArrayList boards;
boards = new ArrayList<>();
boards.add(arduinoWIFI);
boards.add(arduinoUSB);
boards.add(rpiBluetooth);

EmbeddedController controller = new EmbeddedControllerSystem(boards, fs);
controller.run();	

Related files:

• ExampleChamber.java
• Chamber_arduino_USB_DHT22HUM.ino
• Chamber_arduino_WIFI_DHT22TEMP.ino
• Chamber_rpi_BLUETOOTH-HCSR04.py
• Chamber.xml